Advertisements
Advertisements
Question
जाँच कीजिए कि क्या बिंदु (5, -2), (6, 4) और (7,- 2) एक समद्विबाहु त्रिभुज के शीर्ष हैं।
Solution
मान लीजिए कि बिंदु (5, -2), (6, 4) और (7, -2) क्रमशः दिए गए त्रिभुज के शीर्ष A, B और C को दर्शाते हैं।
AB = `sqrt((5-6)^2+(-2-4)^2)`
= `sqrt((-1)^2+(-6)^2)`
= `sqrt(1+36)`
= `sqrt37`
BC = `sqrt((6-7)^2+(4-(-2))^2)`
= `sqrt((-1)^2+(6)^2)`
= `sqrt(1+36)`
= `sqrt37`
CA = `sqrt((5-7)^2+(-2-(-2))^2)`
= `sqrt((-2)^2+0^2)`
= `sqrt(4+0)`
= 2
इसलिए, AB = BC ≠ CA
जैसा दोनों भुजाएँ बराबर लंबाई की हैं, इसलिए ABC एक समद्विबाहु त्रिभुज है।
APPEARS IN
RELATED QUESTIONS
जाँच कीजिए कि बिंदु P(-2, 2), Q(2, 2) और R(2, 7) समकोण त्रिभुज के शीर्षबिंदु हैं।
निम्नलिखित बिंदुओं को जोड़नेवाले रेखाखंड त्रिभुज बना सकते हैं क्या? यदि त्रिभुज बनता हो तो भुजाओं के आधार पर त्रिभुज का प्रकार लिखिए।
L(6, 4), M(-5, -3), N(-6, 8)
x और y में एक ऐसा संबंध ज्ञात कीजिए कि बिंदु (x, y) बिंदुओं (3, 6) और (–3, 4) से समदूरस्थ हो।
बिंदु P(–6, 8) की मूलबिंदु से दूरी ______ है।
शीर्षों (0, 4), (0, 0) और (3, 0) वाले त्रिभुज का परिमाप ______ है।
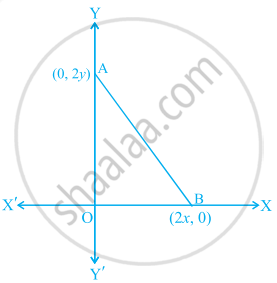
आकृति में दर्शाए गए त्रिभुज AOB के तीनों शीर्षो से समदूरस्थ बिंदु के निर्देशांक ______ हैं।
एक वृत्त का केंद्र मूलबिंदु पर है तथा एक बिंदु P(5, 0) इस वृत्त पर स्थित है। बिंदु Q(6, 8) इस वृत्त के बाहर स्थित है।
बिंदुओं A(–5, 6), B(–4, –2) और C(7, 5) से बनने वाले त्रिभुज का प्रकार बताइए।
बिंदुओं A(2, –2), B(7, 3), C(11, –1) और D(6, –6) को इसी क्रम में लेने पर किस प्रकार का चतुर्भुज बनता है?
एक बिंदु ज्ञात कीजिए, जो A(–5, 4) और B(–1, 6) से समदूरस्थ हो। ऐसे कितने बिंदु हैं?
