Advertisements
Advertisements
Question
ज्ञात कीजिए :
1 से 500 तक के उन पूर्णांकों का योग जो 2 या 5 के गुणज हैं।
[संकेत (iii) : ये संख्याएँ होंगी : 2 के गुणज + 5 के गुणज – 2 और 5 दोनों के गुणज]
Solution
चूँकि, 2 या 5 के गुणज = 2 के गुणज + 5 के गुणज – [एलसीएम (2, 5) के गुणज अर्थात्, 10],
∴ 1 से 500 तक 2 या 5 का गुणज
= 1 से 500 तक 2 के गुणकों की सूची + 1 से 500 तक 5 के गुणकों की सूची – 1 से 500 तक 10 के गुणकों की सूची
= (2, 4, 6,..., 500) + (5, 10, 15,..., 500) – (10, 20,..., 500) ...(i)
ये सभी सूची एक AP बनाती हैं।
अब, पहली सूची में शब्दों की संख्या,
500 = 2 + (n1 – 1)2
⇒ 498 = (n1 – 1)2 ...[∵ a1 = a + (n – 1)d]
⇒ n1 – 1 = 249
⇒ n1 = 250
दूसरी सूची में शब्दों की संख्या,
500 = 5 + (n2 – 1)5
⇒ 495 = (n2 – 1)5 ...[∵ l = 500]
⇒ 99 = (n2 – 1)
⇒ n2 = 100
और तीसरी सूची में पदों की संख्या,
500 = 10 + (n3 – 1)10
⇒ 490 = (n3 – 1)10
⇒ n3 – 1 = 49
⇒ n3 = 50
समीकरण (i) से 1 से,
1 से 500 तक 2 या 5 के गुणजों का योग
= (2, 4, 6,..., 500) का योग + (5, 10,..., 500) का योग – (10, 20,..., 500) का योग
= `n_1/2[2 + 500] + n_2/2[5 + 500] - n_3/2[10 + 500]` ...`[∵ S_n = n/2(a + l)]`
= `(250/2 xx 502) + (100/2 xx 505) - (50/2 xx 510)`
= (250 × 251) + (505 × 50) – (25 × 510)
= 62750 + 25250 – 12750
= 88000 – 12750
= 75250
APPEARS IN
RELATED QUESTIONS
एक A.P. में, a = 5, d = 3 और an = 50 दिया है। n और Sn ज्ञात कीजिए।
एक A.P. में, a = 3, n = 8 और S = 192 दिया है। d ज्ञात कीजिए।
636 योग प्राप्त करने के लिए, AP.: 9, 17, 25, … के कितने पद लेने चाहिए?
0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
केंद्र A से प्रारंभ करते हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm,……. वाले उतरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (Spiral) बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (π = `22/7` लीजिए।)
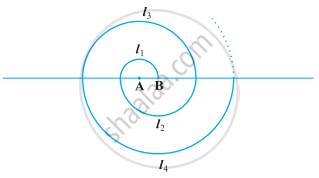
[संकेत: क्रमशः केंद्रों A, B, A, B,... वाले अर्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं।]
प्रथम 100 प्राकृत संख्याओं के योग को ज्ञात करने से संबद्ध प्रसिद्ध गणितज्ञ ______ है।
ज्ञात कीजिए कि 55 एक AP : 7, 10, 13,... का पद है या नहीं। यदि हाँ, तो ज्ञात कीजिए कि यह कौन-सा पद है।
AP: –2, –7, –12,... का कौन-सा पद –77 है? पद –77 तक इस AP का योग ज्ञात कीजिए।
कनिका को उसका जेब खर्च 1 जनवरी 2008 को दिया गया। वह इसमें से अपने पिग्गी बैंक में पहले दिन 1 रु डालती है, दूसरे दिन 2 रु डालती है, तीसरे दिन 3 रु डालती है तथा ऐसा ही महीने के अंत तक करती रहती है। उसने अपने जेब खर्च में से 204 रु खर्च भी किए और पाया कि महीने के अंत में उसके पास अभी भी 100 रु शेष हैं। उस महीने उसको कितना जेब खर्च मिला था ?
100 और 200 के बीच के उन पूर्णांकों का योग ज्ञात कीजिए, जो 9 से विभाज्य नहीं हैं।
[संकेत (ii) : ये संख्याएँ होंगी : कुल संख्याएँ– 9 से विभाज्य संख्याएँ]
