Advertisements
Advertisements
Question
कैसेट बनाने वाली किसी कंपनी के लागत एवं राजस्व फलन क्रमश: C(x) = 26,000 + 30x एवं R(x) = 43x है, जहाँ x एक सप्ताह में निर्मित किए गए एवं बेचे गए कैसेटों की संख्या है। कुछ लाभ अर्जित करने के लिए कंपनी द्वारा कितनी कैसेट अवश्य बेचे जाने चाहिए?
Solution
समझें कि, लागत फलन, C(x) = 2600 + 30x और राजस्व फलन R(x) = 43x
इसलिए, लाभ के लिए, P(x), R(x) > C(x)
∴ 43x > 26000 + 30x
⇒ 26000 + 30 < 43x
⇒ 30x − 43x < −26000
⇒ −13x < −26000
आगे सरलीकृत करें,
⇒ 13x > 26000
⇒ x > 2000
इसलिए, कुछ लाभ के लिए निर्मित किए जाने वाले कैसेट की संख्या इससे अधिक होनी चाहिए।
कुछ लाभ के लिए निर्मित कैसेट की संख्या 2000 से अधिक होनी चाहिए।
APPEARS IN
RELATED QUESTIONS
असमिका 3x – 5 < x + 7 को हल कीजिए जहाँ x एक प्राकृतिक संख्या है।
असमिका 3x – 5 < x + 7 को हल कीजिए जहाँ x एक पूर्णाक है।
|3 – 4x| ≥ 9 को हल कीजिए।
1 ≤ |x – 2| ≤ 3 को हल कीजिए।
किसी उत्पाद के लागत फलन एवं राजस्व फलन क्रमशः C(x) = 20x + 4000 एवं R(x) = 60x + 2000 हैं जहाँ x निर्मित की गईं एवं बेची गईं वस्तुओं की संख्या है। कुछ लाभ अर्जित करने के लिए कितनी वस्तुएँ अवश्य बेची जानी चाहिए?
`(|x + 3| + x)/(x + 2) > 1` को x के लिए हल कीजिए।
यदि `|x - 2|/(x - 2) ≥ 0`, तो
एक आयत की लंबाई उसकी चौड़ाई का तीन गुना है। यदि आयत का न्यूनतम परिमाप 160 सेमी है, तो
x चर वाले असमिका निकाय के हल को नीचे प्रदर्शित संख्या रेखाओं पर निरूपित किया गया है, तो

यदि |x + 3| ≥ 10, तो
यदि –x ≤ –4, तो 2x ______ 8
यदि |3x - 7| > 2, तो x ______ `5/3` या x ______ 3
यदि p > 0 एवं q < 0, तो p + q ______ p
निम्नलिखित असमिका को x के लिए हल कीजिए:
`-5 ≤ (2 - 3x)/4 ≤ 9`
निम्नलिखित असमिका को x के लिए हल कीजिए:
4x + 3 ≥ 2x + 17, 3x – 5 < –2
किसी त्रिभुज की सबसे बड़ी भुजा सबसे छोटी भुजा से दुगनी है एवं तीसरी भुजा सबसे छोटी भुजा से 2 सेमी अधिक है। यदि त्रिभुज का परिमाप 166 सेमी से अधिक है तो सबसे छोटी भुजा की न्यूनतम लंबाई ज्ञात कीजिए।
यदि x < 5, तो
दिया हुआ है कि x, y, b वास्तविक संख्याएँ हैं और x < y, b < 0, तब
यदि x वास्तविक संख्या है और |x| < 3, तो
यदि |x − 1| > 5, तो
यदि |x + 2| ≤ 9, तो
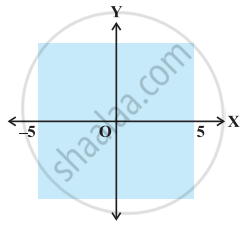
दिए हुए आलेख को प्रदर्शित करने वाली असमिका निम्नलिखित में से कौन-सी है।
बताइए निम्नलिखित कथन सत्य है या असत्य है?
यदि xy > 0, तो x < 0 और y < 0
बताइए निम्नलिखित कथन सत्य है या असत्य है?
यदि xy < 0, तो x < 0 और y < 0
