Advertisements
Advertisements
Question
किसी त्रिभुज के अभ्यांतर में एक ऐसा बिंदु ज्ञात कीजिए जो त्रिभुज की सभी भुजाओं से समदूरस्थ हो।
Solution
वह बिंदु जो त्रिभुज की सभी भुजाओं से समान दूरी पर होता है, त्रिभुज का अंतःकेंद्र कहलाता है। किसी त्रिभुज का अंतःकेंद्र उस त्रिभुज के आंतरिक कोणों के कोण समद्विभाजक का प्रतिच्छेदन बिंदु होता है।
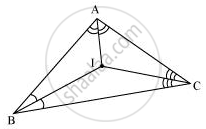
यहाँ, ΔABC में, हम इस त्रिभुज के अंतः कोणों के कोण समद्विभाजक खींचकर इस त्रिभुज का अंत:केंद्र ज्ञात कर सकते हैं। I वह बिंदु है जहां ये कोण समद्विभाजक एक दूसरे को काट रहे हैं। अतः, ΔABC की सभी भुजाओं से समदूरस्थ बिंदु I है।
APPEARS IN
RELATED QUESTIONS
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है।
आकृति में, ∆ABC की भुजाओं AB और AC को क्रमशः बिंदुओं P और Q तक बढ़ाया गया है। साथ ही, ∠PBC < ∠QCB, है। दर्शाइए कि: AC > AB है।
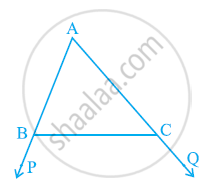
आकृति में, ∠B < ∠A और ∠C < ∠D है। दर्शाइए कि: AD < BC है।

AB और CD एक चतुर्भुज ABCD की क्रमशः सबसे छोटी और सबसे लंबी भुजाएँ हैं (देखिए आकृति)। दर्शाइए कि ∠A > ∠C और ∠B > ∠D है।

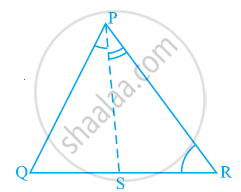
आकृति में, PR > PQ है और PS कोण QPR को समद्विभाजित करता है। सिद्ध कीजिए कि ∠PSR > ∠PSQ है।
दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखंड खींचे जा सकते हैं उनमें लंब रेखाखंड सबसे छोटा होता है।
ABC एक त्रिभुज है। इसके अभ्यांतर में एक ऐसा बिंदु ज्ञात कीजिए जो ∆ABC के तीनों शीर्षों से समदूरस्थ है।
एक बड़े पार्क में लोग तीन बिंदुओं (स्थानों) पर केंद्रित हैं (देखिए आकृति)।

A: जहाँ बच्चों के लिए फिसल पट्टी और झूले हैं।
B: जिसके पास मानव-निर्मित एक झील है।
C: जो एक बड़े पार्किंग स्थल और बाहर निकलने के रास्ते के निकट है।
एक आइसक्रीम का स्टाल कहाँ लगाना चाहिए ताकि वहाँ लोगों की अधिकतम संख्या पहुँच सके?
(संकेत: स्टॉल को A, B और C से समान दूरी पर होना चाहिए)
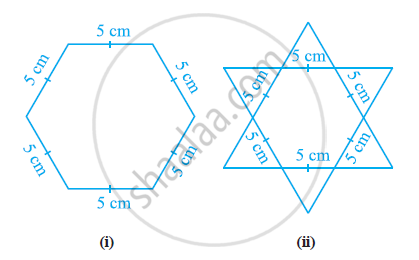
षट्भुजीय और तारे के आकार की रंगोलियों (देखिए आकृति (i) और (ii)] को 1 सेमी भुजा वाले समबाहु त्रिभुजों से भरकर पूरा कीजिए। प्रत्येक स्थिति में, त्रिभुजों की संख्या गिनिए। किसमें अधिक त्रिभुज हैं?
“यदि किसी त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोण और एक भुजा के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
