Advertisements
Advertisements
Question
Line segment joining the mid-points M and N of parallel sides AB and DC, respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD = BC.
Solution
Given: In trapezium ABCD, points M and N are the mid-points of parallel sides AB and DC respectively and join MN, which is perpendicular to AB and DC.
To prove: AD = BC
Proof: Since, M is the mid-point of AB.
∴ AM = MB
Now, in ΔAMN and ΔBMN,
AM = MB ...[Proved above]
∠3 = ∠4 ...[Each 90°]
MN = MN ...[Common side]
∴ ΔAMN ≅ ΔBMN ...[By SAS congruence rule]
∴ ∠1 = ∠2 ...[By CPCT]
On multiplying both sides of above equation by –1 and then adding 90° both sides, we get
90° – ∠1 = 90° – ∠2
⇒ ∠AND = ∠BNC ...(i)
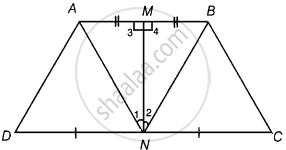
Now, in ΔADN and ΔBCN,
∠AND = ∠BNC ...[From equation (i)]
AN = BN ...[∵ΔAMN ≅ ΔBMN]
And DN = NC ...[∵ N is the mid-point of CD (given)]
∴ ΔADN ≅ ΔBCN ...[By SAS congruence rule]
Hence, AD = BC ...[By CPCT]
Hence proved.
APPEARS IN
RELATED QUESTIONS
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
ABC is an isosceles triangle with AB = AC. Drawn AP ⊥ BC to show that ∠B = ∠C.
Prove that in a quadrilateral the sum of all the sides is greater than the sum of its diagonals.
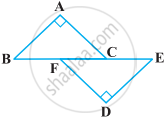
In the following figure, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that ∆ABC ≅ ∆DEF.
ABC and DBC are two triangles on the same base BC such that A and D lie on the opposite sides of BC, AB = AC and DB = DC. Show that AD is the perpendicular bisector of BC.
ABC is an isosceles triangle in which AC = BC. AD and BE are respectively two altitudes to sides BC and AC. Prove that AE = BD.
In a right triangle, prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse.
ABCD is a quadrilateral such that diagonal AC bisects the angles A and C. Prove that AB = AD and CB = CD.
ABCD is quadrilateral such that AB = AD and CB = CD. Prove that AC is the perpendicular bisector of BD.
