Advertisements
Advertisements
Question
Match the following sets for all sets A, B, and C.
| Column A | Column B |
| (i) ((A′ ∪ B′) – A)′ | (a) A – B |
| (ii) [B′ ∪ (B′ – A)]′ | (b) A |
| (iii) (A – B) – (B – C) | (c) B |
| (iv) (A – B) ∩ (C – B) | (d) (A × B) ∩ (A × C) |
| (v) A × (B ∩ C) | (e) (A × B) ∪ (A × C) |
| (vi) A × (B ∪ C) | (f) (A ∩ C) – B |
Solution
| Column A | Answer |
| (i) ((A′ ∪ B′) – A)′ | (b) A |
| (ii) [B′ ∪ (B′ – A)]′ | (c) B |
| (iii) (A – B) – (B – C) | (a) A – B |
| (iv) (A – B) ∩ (C – B) | (f) (A ∩ C) – B |
| (v) A × (B ∩ C) | (d) (A × B) ∩ (A × C) |
| (vi) A × (B ∪ C) | (e) (A × B) ∪ (A × C) |
Explanation:
(i) ((A′ ∪ B′) – A)′
[(A′ ∪ B′) – A]′
= [(A′ ∪ B′) ∩ A’]’ ......{∵ A – B = A ∩ B’}
= [(A ∩ B)’ ∩ A’]’ ......{∵ (A ∩ B)’ = A’ ∪ B’}
= [(A ∩ B)’]’ ∪ (A’)’
= (A ∩ B) ∪ A
= A
((A′ ∪ B′) – A)′ = A
(ii) [B′ ∪ (B′ – A)]′
[B′ ∪ (B′ – A)]′
= (B’)’ ∩ (B’ – A)’ ......{∵ (A ∪ B)’ = A’ ∩ B’}
= B ∩ (B’ ∩ A’)’ ......{∵ A – B = A ∩ B’}
= B ∩ [(B’)’ ∪ (A’)’] ......{∵ (A ∩ B)’ = A’ ∪ B’}
= B ∩ (B ∪ A)
= B
[B′ ∪ (B′ – A)]′ = B
(iii) (A – B) – (B – C)
Step 1:
A – B
Step 2: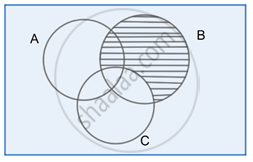
B – C
Step 3: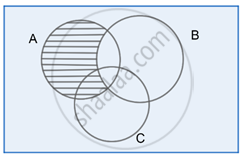
(A – B) – (B – C)
Clearly, the Venn diagram in Step 3 shows same region as in Step 1
Hence, (A – B) – (B – C) = A – B
(iv) (A – B) ∩ (C – B)
Step 1: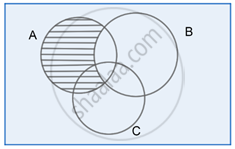
A – B
Step 2: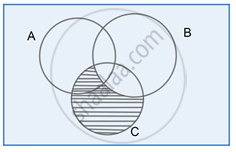
C – B
Step 3: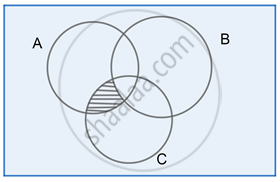
(A – B) ∩ (B – C)
Clearly, from the Venn diagram in Step 3:
(A – B) ∩ (B – C) = A ∩ C – B
(v) A × (B ∩ C)
Let y ∈ A × (B ∩ C)
⇒ y ∈ A and y ∈ (B ∩ C)
⇒ y ∈ A and (y ∈ B and y ∈ C)
⇒ (y ∈ A and y ∈ B) and (y ∈ A and y ∈ C)
⇒ y ∈ (A × B) and y ∈ (A × C)
⇒ y ∈ (A × B) ∩ (A × C)
A × (B ∩ C) = (A × B) ∩ (A × C)
(vi) A × (B ∪ C)
Let y ∈ A × (B ∪ C)
⇒ y ∈ A and y ∈ (B ∪ C)
⇒ y ∈ A and (y ∈ B or y ∈ C)
⇒ (y ∈ A and y ∈ B) or (y ∈ A and y ∈ C)
⇒ y ∈ (A × B) or y ∈ (A × C)
⇒ y ∈ (A × B) ∪ (A × C)
A × (B ∪ C) = (A × B) ∪ (A × C)
APPEARS IN
RELATED QUESTIONS
What universal set (s) would you propose for the following:
The set of right triangles.
Given the sets, A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, the following may be considered as universal set (s) for all the three sets A, B and C?
{0, 1, 2, 3, 4, 5, 6}
Given the sets, A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, the following may be considered as universal set (s) for all the three sets A, B and C?
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Given the sets A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, the following may be considered as universal set (s) for all the three sets A, B and C?
{1, 2, 3, 4, 5, 6, 7, 8}
If U = {2, 3, 5, 7, 9} is the universal set and A = {3, 7}, B = {2, 5, 7, 9}, then prove that:
\[\left( A \cup B \right)' = A' \cap B'\]
For any two sets A and B, prove that
B ⊂ A ∪ B
For any two sets A and B, prove that
A ∩ B ⊂ A
For any two sets A and B, show that the following statements are equivalent:
(i) \[A \subset B\]
(ii) \[A \subset B\]=ϕ
(iii) \[A \cup B = B\]
(iv) \[A \cap B = A .\]
For three sets A, B and C, show that \[A \cap B = A \cap C\]
For any two sets, prove that:
\[A \cap \left( A \cup B \right) = A\]
If A and B are sets, then prove that \[A - B, A \cap B \text{ and } B - A\] are pair wise disjoint.
Using properties of sets, show that for any two sets A and B,\[\left( A \cup B \right) \cap \left( A \cap B' \right) = A\]
For any two sets of A and B, prove that:
\[A' \cup B = U \Rightarrow A \subset B\]
For any two sets of A and B, prove that:
\[B' \subset A' \Rightarrow A \subset B\]
Is it true that for any sets A and \[B, P \left( A \right) \cup P \left( B \right) = P \left( A \cup B \right)\]? Justify your answer.
Each set X, contains 5 elements and each set Y, contains 2 elements and \[\cup^{20}_{r = 1} X_r = S = \cup^n_{r = 1} Y_r\] If each element of S belong to exactly 10 of the Xr's and to eactly 4 of Yr's, then find the value of n.
For any two sets A and B, prove the following:
\[A - B = A \Delta\left( A \cap B \right)\]
Let U be the universal set containing 700 elements. If A, B are sub-sets of U such that \[n \left( A \right) = 200, n \left( B \right) = 300 \text{ and } \left( A \cap B \right) = 100\].Then \[n \left( A' \cap B' \right) =\]
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}; find
B ∪ D
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}; find
A ∪ B ∪ C
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}; find
B ∪ C ∪ D
If X and Y are subsets of the universal set U, then show that X ⊂ Y ⇒ X ∩ Y = X
If A and B are subsets of the universal set U, then show that A ⊂ A ∪ B
If A and B are subsets of the universal set U, then show that (A ∩ B) ⊂ A
A, B and C are subsets of Universal Set U. If A = {2, 4, 6, 8, 12, 20} B = {3, 6, 9, 12, 15}, C = {5, 10, 15, 20} and U is the set of all whole numbers, draw a Venn diagram showing the relation of U, A, B and C.
In a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers. Find the number of families which buy newspaper A only.
In a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers. Find the number of families which buy none of A, B and C
The set (A ∩ B′)′ ∪ (B ∩ C) is equal to ______.
