Advertisements
Advertisements
Question
ΔMNT ~ ΔQRS बिंदू T पासून काढलेल्या शिरोलंबाची लांबी 5 असून बिंदू S पासून काढलेल्या शिरोलंबाची लांबी 9 आहे, तर `("A"(Δ"MNT"))/("A"Δ("QRS"))` हे गुणोत्तर काढा.
Solution
ΔMNT ~ ΔQRS ...[पक्ष]
∴ ∠M ≅ ∠Q .....(i) [समरूप त्रिकोणांचे संगत कोन]
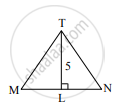
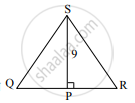
ΔMLT व ΔQPS मध्ये,
∠M ≅ ∠Q .....[(i) वरून]
∠MLT ≅ ∠QPS ....[प्रत्येक कोनाचे माप 90°]
∴ ΔMLT ~ ΔQPS ...[समरूपतेची कोको कसोटी]
∴ `"MT"/"QS" = "TL"/"SP"` ....[समरूप त्रिकोणांच्या संगत बाजू]
∴ `"MT"/"QS" = 5/9` ...(ii)
आता, ΔMNT ~ ΔQRS ...[पक्ष]
∴ `("A"(Δ"MNT"))/("A"(Δ"QRS")) = "MT"^2/"QS"^2` ..[समरूप त्रिकोणांच्या क्षेत्रफळांचे प्रमेय]
= `("MT"/"QS")^2`
= `(5/9)^2` ....[(ii) वरून]
∴ `("A"(Δ"MNT"))/("A"(Δ"QRS")) = 25/81`
APPEARS IN
RELATED QUESTIONS
एका त्रिकोणाचा पाया 9 आणि उंची 5 आहे. दुसऱ्या त्रिकोणाचा पाया 10 आणि उंची 6 आहे, तर त्या त्रिकोणांच्या क्षेत्रफळांचे गुणोत्तर काढा.
दिलेल्या आकृती मध्ये BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8 तर `("A(ΔABC)")/("A(ΔADB)")` काढा.

दिलेल्या आकृती मध्ये रेख PS ⊥ रेख RQ रेख QT ⊥ रेख PR. जर RQ = 6, PS = 6, PR = 12 तर QT काढा.
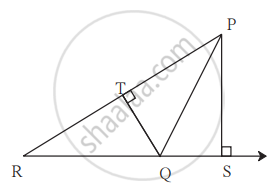
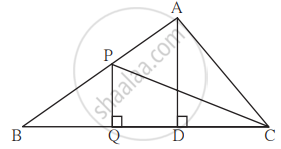
दिलेल्या आकृतीत, PQ ⊥ BC, AD ⊥ BC तर खालील गुणोत्तरे लिहा.
i) `"A(ΔPQB)"/"A(ΔPBC)"`
ii) `"A(ΔPBC)"/"A(ΔABC)"`
iii) `"A(ΔABC)"/"A(ΔADC)"`
iv) `"A(ΔADC)"/"A(ΔPQC)"`
ΔABC मध्ये B - D – C आणि BD = 7, BC = 20 तर खालील गुणोत्तरे काढा.
- `("A"(Δ"ABD"))/("A"(Δ"ADC"))`
- `("A"(Δ"ABD"))/("A"(Δ"ABC"))`
- `("A"(Δ"ADC"))/("A"(Δ"ABC"))`
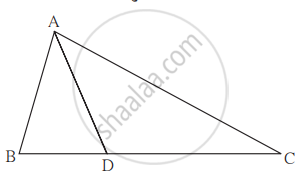
आकृतीमध्ये BD = 8, BC = 12 B-D-C, तर `("A"(Delta"ABC"))/("A"(Delta"ABD"))` = ?
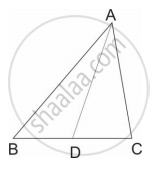
∆PQR ~ ∆SUV, तर त्या त्रिकोणाच्या एकरूप कोनांच्या जोड्या लिहा.
आकृतीमध्ये, AB लंब BC आणि DC लंब BC, AB = 6, DC = 4, तर `("A"(Delta"ABC"))/("A"(Delta"BCD"))` = ?
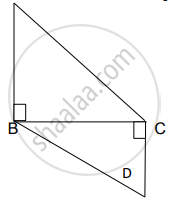
आकृतीमध्ये, दिलेल्या माहितीवरून ∠ABC = 90°, ∠DCB = 90°, AB = 6, DC = 8, तर `("A"(Delta"ABC"))/("A"(Delta"BCD"))` किती?
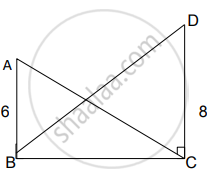
∆ABC मध्ये, B-D-C आणि BD = 7, BC = 20, तर खालील गुणोत्तर काढा.
`(A(∆ABD))/(A(∆ABC))`
