Advertisements
Advertisements
Question
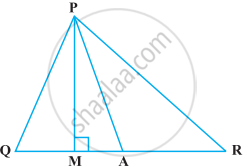
निम्नलिखित आकृति में, ∠Q > ∠R, PA कोण ∠QPR का समद्विभाजक है तथा PM ⊥ QR है। सिद्ध कीजिए कि ∠APM = `1/2` (∠Q – ∠R) है।
Solution
त्रिभुज PQR में दिया गया है, ∠Q > ∠R, PA, ∠QPR और PM ⊥ QR का समद्विभाजक है।
साबित करने के लिए कि ∠APM = `1/2` (∠Q – ∠R)
उपपत्ति - PA, ∠QPR का समद्विभाजक है।
इसलिए, ∠QPA = ∠APR
कोण PQM में, ∠Q + ∠PMQ + ∠QPM = 180° ...(I) [त्रिभुज के कोणों के योग का गुण]
∠Q + 90° + ∠QPM = 180° ...[∠PMR = 90°]
∠Q = 90° – ∠QPM ...(II)
त्रिभुज PMR में, ∠PMR + ∠R + ∠RPM = 180° ...[त्रिभुज के कोणों के योग का गुण]
90° + ∠R + ∠RPM = 180° ...[∠PMR = 90°]
∠R = 180° – 90° – ∠RPM
∠R = 90° – ∠RPM ...(III)
समीकरण (III) को समीकरण (II) से घटाने पर, हम पाते हैं।
∠Q – ∠R = (90° – ∠APM) – (90° – ∠RPM)
∠Q – ∠R = ∠RPM – ∠QPM
∠Q – ∠R = (∠RPA + ∠APM) – (∠QPA – ∠APM) ...(IV)
∠Q – ∠R = ∠QPA + ∠APM – ∠QPA + ∠APM ...[As, ∠RPA = ∠QPA]
∠Q – ∠R = 2∠APM
∠APM = `1/2` (∠Q – ∠R)
अतः, सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
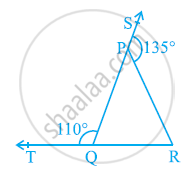
आकृति में, ΔPQR की भुजाओं QP और RQ को क्रमश: बिन्दुओं S और T तक बढाया गया है | यदि ∠SPR = 135° है और ∠PQT = 110° है, तो ∠PRQ ज्ञात कीजिए|
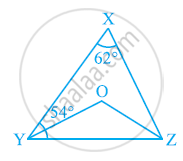
आकृत में, ∠X = 62° और XYZ = 54° है | यदि YO और ZO क्रमश: Δ XYZ के ∠XYZ और ∠XZY के समद्विभाजक है, तो ∠OZY और ∠YOZ ज्ञात कीजिए |
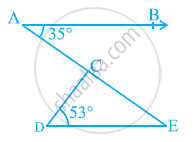
आकृति में, यदि AB || DE, ∠BAC = 35° और ∠CDE = 53° है तो ∠ DCE ज्ञात कीजिए |
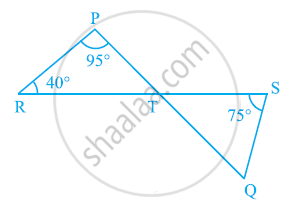
आकृति में, यदि रेखाएँ PQ और RS बिंदु T पर इस प्रकार प्रतिच्छेद करती है कि ∠PRT = 40°, ∠RPT = 95° और ∠TSQ = 75° है तो ∠SQT ज्ञात कीजिए |
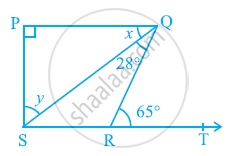
आकृति में, यदि PQ ⊥ PS, PQ || SR, ∠ SQR = 28° और ∠QRT = 65° है, तो x और y के मान ज्ञात कीजिए |
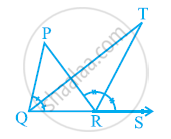
आकृति में, Δ PQR कि भुजा QR को बिंदु S तक बढाया गया है | यदि ∠PQR और ∠ PRS के समद्विभाजक बिंदु T पर मिलते है, तो सिद्ध कीजिए कि ∠QTR = `1/2` ∠ QPR है |
सिद्ध कीजिए कि एक त्रिभुज के कम से कम दो न्यूनकोण अवश्य होने चाहिए।
