Question

Obtain an expression for the orbital magnetic moment of an electron rotating about the nucleus in an atom.

Answer 1

In the Bohr model of a hydrogen atom, the electron of charge - e performs a uniform circular motion around the positively charged nucleus. Let r, v and T be the orbital radius, speed and period of motion of the electron. Then,

T = `(2pi"r")/"v"`       ...(1)

Therefore, the orbital magnetic moment associated with this orbital current loop has a magnitude,

I = `"e"/"T" = "ev"/(2pi"r")`    ...(2)

Therefore, the magnetic dipole moment associated with this electronic current loop has a magnitude

M₀ = current × area of the loop

`= "l"(pi"r"^2) = "ev"/(2pi"r") xx pi"r"^2 = 1/2 "evr"`    ....(3)

Multiplying and dividing the right-hand side of the above expression by the electron mass m_e,

`"M"_0 = "e"/(2"m"_"e") ("m"_"e""vr") = "e"/(2"m"_"e") "L"_0`     ....(4)

where L₀ - m_evr is the magnitude of the orbital angular momentum of the electron. `vec"M"_0` is opposite to `vec"L"_0`.

∴ `vec"M"_0 = - "e"/(2"m"_"e") vec"L"_0`      ....(5)

which is the required expression. →

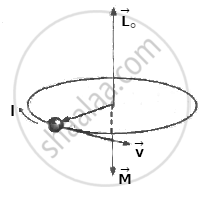
According to Bohr's second postulate of stationary orbits in his theory of hydrogen atom, the angular momentum of the electron in the nth stationary orbit is equal to n `"h"/(2pi)`, where h is the Planck constant and n is a positive integer. Thus, for an orbital electron,

`"L"_0 = "m"_"e" "vr" = ("nh")/(2pi)`    ...(6)

Substituting for L₀ in Eq. (4),

`"M"_0 = "enh"/(4pi"m"_"e")`

For n = 1, M₀ = `"eh"/(4pi"m"_"e")`

The quantity `"eh"/(4pi"m"_"e")` is a fundamental constant called the Bohr magneton,

`therefore mu_"B" * mu_"B"`

`= 9.274 xx 10^-24 "J"//"T"` (or Am²)

= 5.788 x 10^-5 eV/T.

Answer 2

Expression for magnetic dipole moment:

1. Consider an electron of mass me and charge e revolving in a circular orbit of radius r around the positive nucleus in a clockwise direction, leading to an anticlockwise current.
   
   U.C.M of an electron around the nucleus
2. If the electron travels a distance 2πr in time T then, its orbital speed v = 2πr/T
3. The magnitude of circulating current is given by,
   I = e`(1/"T")`
   But, T = `(2pi"r")/"v"`
   ∴ I = e`(1/(2pir"/""v")) = "ev"/(2pi"r")`
4. The orbital magnetic moment associated with the orbital current loop is given by,
   m_orb = IA = `"ev"/(2pi"r") xx pi"r"^2` [∵ Area of current loop, A = πr²]
   ∴ m_orb = `"evr"/2` ….(1)
5. The angular momentum of an electron due to its orbital motion is given by, 
   L = m_evr 
6. Multiplying and dividing the R.H.S of equation (1) by m_e, 
   m_orb = `"e"/(2"m"_"e") xx "m"_"e""vr"`
   ∴ m_orb = `"eL"/(2"m"_"e")`
7. This equation shows that the orbital magnetic moment is proportional to the angular momentum. But as the electron bears a negative charge, the orbital magnetic moment and orbital angular momentum are in opposite directions and perpendicular to the plane of the orbit.
   Using vector notation, `vec"m"_"orb" = -("e"/(2"m"_"e"))vec"L"` 

Answer 3

Consider an electron moving with constant speed v in a circular orbit of radius r about the nucleus as shown in the figure.

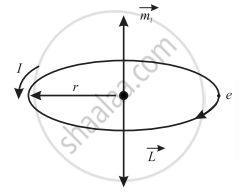
If the electron travels a distance of 2πr (circumference) in time T, then its orbital speed, `v=(2pir)/T`.

Thus the current I associated with this orbiting electron of charge e is

`I = e/T`

`T = (2pi)/omega and omega=v/r`, the angular speed 

`I = (eomega)/(2pi)=(ev)/(2pir)`

The orbital magnetic moment associated with orbital current loop is

`m_("orb")=IA=(ev)/(2pir)xxpir^2`

`=1/2evr`