Advertisements
Advertisements
Question
Obtain Bohr’s quantisation condition for angular momentum of electron orbiting in nth orbit in hydrogen atom on the basis of the wave picture of an electron using de Broglie hypothesis.
Solution 1
`n lambda = 2 pi r`
But ` lambda = n/(mv) `( By De Broglie)
`(n lambda) /(mv) = 2 pi r`
` therefore (lambda n) /(2 pi ) = mvr ` (mvr = L)
` therefore L = (lambda n)/(2 pi)`
Solution 2
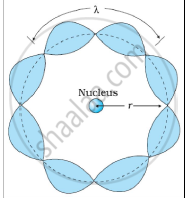
Bohr's second postulate states that the angular momentum of an electron has only those values that are integral multiples of `"h"/(2pi)` He thought that the motion of electrons within an atom is associated with the standing wave along the orbit as shown.
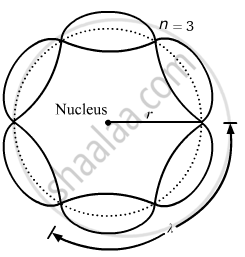
About standing waves in stretched strings, we know that only those waves survive for which the distances traveled in the round trip between the ends are integral multiples of the wavelength. Similarly, for an electron moving in the nth orbit of radius rn, the distance traveled in one trip is 2πrn, which should be an integral multiple of the wavelength.
2πrn = nλ (where n= 1, 2, 3, 4 etc)
By de-Broglie hypothesis, we have:
`lambda = "h"/"p" = "h"/("mv"_"n")`
Substituting the value of λ in the above expression, we get:
`2pi"r"_"n" = "n" "h"/"mv"_"n"`
⇒ `"mv"_"n""r"_"n" = "n" "h"/(2pi)`
Angular momentum `= "L" = "n" "h"/(2pi)`
RELATED QUESTIONS
Balmer series was observed and analysed before the other series. Can you suggest a reason for such an order?
Suppose, the electron in a hydrogen atom makes transition from n = 3 to n = 2 in 10−8 s. The order of the torque acting on the electron in this period, using the relation between torque and angular momentum as discussed in the chapter on rotational mechanics is
Radiation from hydrogen discharge tube falls on a cesium plate. Find the maximum possible kinetic energy of the photoelectrons. Work function of cesium is 1.9 eV.
When the electron orbiting in hydrogen atom in its ground state moves to the third excited state, show how the de Broglie wavelength associated with it would be affected.
The radius of the third Bohr orbit for hydrogen atom is ____________.
According to the Bohr theory of H-atom, the speed of the electron, its energy and the radius of its orbit varies with the principal quantum number n, respectively, as:
An ionised H-molecule consists of an electron and two protons. The protons are separated by a small distance of the order of angstrom. In the ground state ______.
- the electron would not move in circular orbits.
- the energy would be (2)4 times that of a H-atom.
- the electrons, orbit would go around the protons.
- the molecule will soon decay in a proton and a H-atom.
When an electron falls from a higher energy to a lower energy level, the difference in the energies appears in the form of electromagnetic radiation. Why cannot it be emitted as other forms of energy?
The number of times larger the spacing between the energy levels with n = 3 and n = 8 spacing between the energy level with n = 8 and n = 9 for the hydrogen atom is ______.
Find the ratio of energies of photons produced due to transition of an election of hydrogen atom from its (i) second permitted energy level to the first level. and (ii) the highest permitted energy level to the first permitted level.
