Advertisements
Advertisements
Question
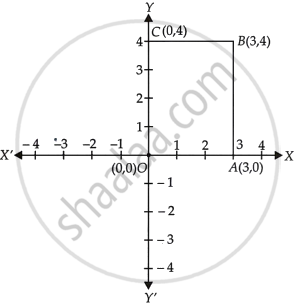
On plotting the points O(0, 0), A(3, 0), B(3, 4), C(0, 4) and joining OA, AB, BC and CO which of the following figure is obtained?
Options
Square
Rectangle
Trapezium
Rhombus
Solution
Rectangle
Explanation:
Given, point O(0, 0) is the origin.
A(3, 0) lies on positive direction of x-axis, B(3, 4) lies in 1st quadrant and C(0, 4) lies on positive direction of y-axis.
On joining OA, AB, BC and CO the figure obtained is a rectangle, which is shown as follows:
RELATED QUESTIONS
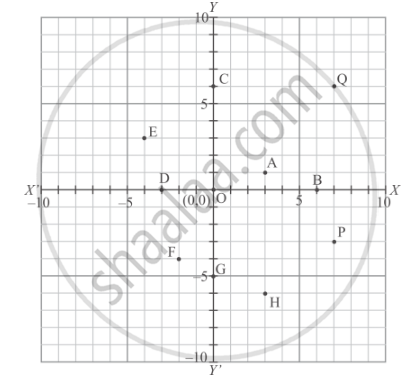
Write the coordinates of each of the following points marked in the graph paper:
Plot the following point on the graph paper:
(7, −4)
Plot the following point on the graph paper:
(7, 0)
Some points are shown in the following figure. With the help of it answer the following questions:
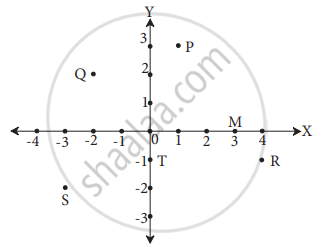
- Write the co-ordinates of the points Q and R.
- Write the co-ordinates of the points T and M.
- Which point lies in the third quadrant?
- Which are the points whose x and y co-ordinates are equal?
Plot the following point in the coordinate system and identify the quadrant.
R(−6, −7)
Plot the following points in the coordinate plane. Join them in order. What type of geometrical shape is formed?
(0, 0) (−4, 0) (−4, −4) (0, −4)
If the y-coordinate of a point is zero, then the point always lies ______
Find the quadrants without plotting the point on a graph sheet
(3, −4)
Plot the following point in a graph sheet.
A(5, 2)
Plot the following point in a graph sheet.
B(−7, −3)
Find the quadrants without plotting the point on a graph sheet.
(2, 0)
Plot the following point in a graph sheet.
E(0, −5)
Find the quadrants without plotting the point on a graph sheet.
(−8, 0)
Plot the following point in a graph sheet.
K(0, 7)
If P(5, 1), Q(8, 0), R(0, 4), S(0, 5) and O(0, 0) are plotted on the graph paper, then the point(s) on the x-axis are ______.
Plot the points (x, y) given by the following table. Use scale 1 cm = 0.25 units
| x | 1.25 | 0.25 | 1.5 | – 1.75 |
| y | – 0.5 | 1 | 1.5 | – 0.25 |
Points A(5, 3), B(– 2, 3) and D(5, – 4) are three vertices of a square ABCD. Plot these points on a graph paper and hence find the coordinates of the vertex C.
Plot the points A(1, – 1) and B(4, 5). Draw a line segment joining these points. Write the coordinates of a point on this line segment between the points A and B.
Plot the points A(1, – 1) and B(4, 5). Extend this line segment and write the coordinates of a point on this line which lies outside the line segment AB.
