Advertisements
Advertisements
Question
Keeping the number of moles, volume and temperature the same, which of the following are the same for all ideal gases?
Options
Rms speed of a molecule
Density
Pressure
Average magnitude of momentum.
Solution
Pressure
Pressure of an ideal gas is given by PV = \[\frac{1}{3}mn u^2\] .
APPEARS IN
RELATED QUESTIONS
Which of the following quantities is zero on an average for the molecules of an ideal gas in equilibrium?
The average momentum of a molecule in a sample of an ideal gas depends on
Calculate the volume of 1 mole of an ideal gas at STP.
Let Q and W denote the amount of heat given to an ideal gas and the work done by it in an isothermal process.
Let Q and W denote the amount of heat given to an ideal gas and the work done by it in an adiabatic process.
(a) Q = 0
(b) W = 0
(c) Q = W
(d) Q ≠ W
A rigid container of negligible heat capacity contains one mole of an ideal gas. The temperature of the gas increases by 1° C if 3.0 cal of heat is added to it. The gas may be
(a) helium
(b) argon
(c) oxygen
(d) carbon dioxide
The figure shows a cylindrical container containing oxygen (γ = 1.4) and closed by a 50-kg frictionless piston. The area of cross-section is 100 cm2, atmospheric pressure is 100 kPa and g is 10 m s−2. The cylinder is slowly heated for some time. Find the amount of heat supplied to the gas if the piston moves out through a distance of 20 cm.
An amount Q of heat is added to a monatomic ideal gas in a process in which the gas performs a work Q/2 on its surrounding. Find the molar heat capacity for the process
Two ideal gases have the same value of Cp / Cv = γ. What will be the value of this ratio for a mixture of the two gases in the ratio 1 : 2?
An ideal gas at pressure 2.5 × 105 Pa and temperature 300 K occupies 100 cc. It is adiabatically compressed to half its original volume. Calculate (a) the final pressure (b) the final temperature and (c) the work done by the gas in the process. Take γ = 1.5
Consider a given sample of an ideal gas (Cp/Cv = γ) having initial pressure p0 and volume V0. (a) The gas is isothermally taken to a pressure p0/2 and from there, adiabatically to a pressure p0/4. Find the final volume. (b) The gas is brought back to its initial state. It is adiabatically taken to a pressure p0/2 and from there, isothermally to a pressure p0/4. Find the final volume.
1 litre of an ideal gas (γ = 1.5) at 300 K is suddenly compressed to half its original volume. (a) Find the ratio of the final pressure to the initial pressure. (b) If the original pressure is 100 kPa, find the work done by the gas in the process. (c) What is the change in internal energy? (d) What is the final temperature? (e) The gas is now cooled to 300 K keeping its pressure constant. Calculate the work done during the process. (f) The gas is now expanded isothermally to achieve its original volume of 1 litre. Calculate the work done by the gas. (g) Calculate the total work done in the cycle.
Two vessels A and B of equal volume V0 are connected by a narrow tube that can be closed by a valve. The vessels are fitted with pistons that can be moved to change the volumes. Initially, the valve is open and the vessels contain an ideal gas (Cp/Cv = γ) at atmospheric pressure p0 and atmospheric temperature T0. The walls of vessel A are diathermic and those of B are adiabatic. The valve is now closed and the pistons are slowly pulled out to increase the volumes of the vessels to double the original value. (a) Find the temperatures and pressures in the two vessels. (b) The valve is now opened for sufficient time so that the gases acquire a common temperature and pressure. Find the new values of the temperature and pressure.
The figure shows an adiabatic cylindrical tube of volume V0 divided in two parts by a frictionless adiabatic separator. Initially, the separator is kept in the middle, an ideal gas at pressure p1 and temperature T1 is injected into the left part and another ideal gas at pressure p2 and temperature T2 is injected into the right part. Cp/Cv = γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.

A cubic vessel (with faces horizontal + vertical) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of 500 ms–1 in vertical direction. The pressure of the gas inside the vessel as observed by us on the ground ______.
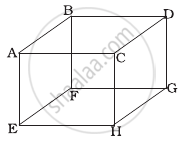
1 mole of an ideal gas is contained in a cubical volume V, ABCDEFGH at 300 K (Figure). One face of the cube (EFGH) is made up of a material which totally absorbs any gas molecule incident on it. At any given time ______.
In a diatomic molecule, the rotational energy at a given temperature ______.
- obeys Maxwell’s distribution.
- have the same value for all molecules.
- equals the translational kinetic energy for each molecule.
- is (2/3)rd the translational kinetic energy for each molecule.
When an ideal gas is compressed adiabatically, its temperature rises: the molecules on the average have more kinetic energy than before. The kinetic energy increases ______.
- because of collisions with moving parts of the wall only.
- because of collisions with the entire wall.
- because the molecules gets accelerated in their motion inside the volume.
- because of redistribution of energy amongst the molecules.
