Advertisements
Advertisements
Question
Plot the points (3, 5) and (− 1, 3) on a graph paper and verify that the straight line passing
through these points also passes through the point (1, 4).
Solution
The points given in the graph:
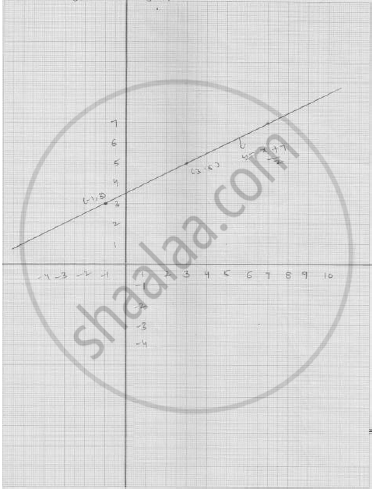
It is clear from the graph the straight lines passes through these points also pass a through
( 1,4 ) .
APPEARS IN
RELATED QUESTIONS
Draw the graph of the following linear equations in two variables:- 3 = 2x + y
From the choices given below, choose the equation whose graph is given in Fig. below.
(i) y = x (ii) x + y = 0 (iii) y = 2x (iv) 2 + 3y = 7x

[Hint: Clearly, (-1, 1) and (1, -1) satisfy the equation x + y = 0]
Draw the graph of the equatio ` x / y + y /4 = 1` Also, find the area of the triangle formed by the
line and the co-ordinates axes.
Draw the graph for the equation, given below :
y + 7 = 0
Draw the graph for the equation given below; hence find the co-ordinates of the points where the graph is drawn meets the co-ordinates axes:
`(1)/(3) x +(1)/(5) y = 1`.
Use graph paper for this question. Draw the graph of 2x - y - 1 = 0 and 2x + y = 9 on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 points per line. Write down the coordinates of the point of intersection of the two lines.
Using a scale of 1 cm to 1 unit for both the axes, draw the graphs of the following equations: 6y = 5x + 10, y = 5x - 15.
From the graph find :
(i) the coordinates of the point where the two lines intersect;
(ii) the area of the triangle between the lines and the x-axis.
Draw the graphs of the following linear equations:
3x + 2y - 6 = 0
Draw the graph for the following
3x + 2y = 14
The graph given below represents the linear equation x = 3 (see figure).

