Advertisements
Advertisements
Question
Plot point A(5, -7). From point A, draw AM perpendicular to the x-axis and AN perpendicular to the y-axis. Write the coordinates of points M and N.
Solution
Given A(5, -7)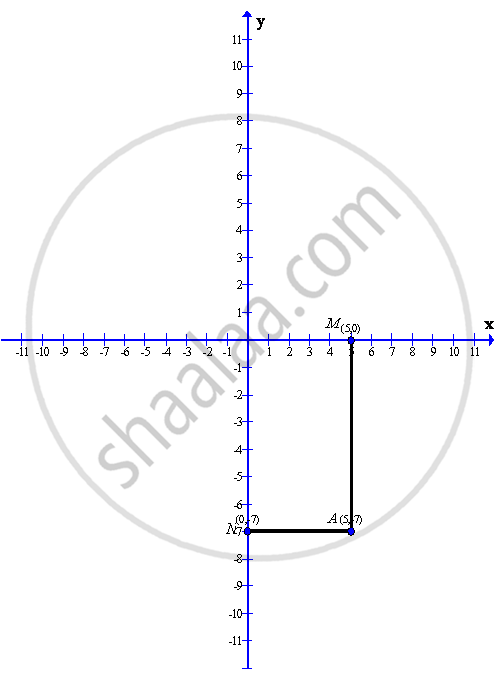
After plotting the given point A(5,-7) on a graph paper. Now let us draw a perpendicular AM from the point A(5,-7) on the x-axis and a perpendicular AN from the point A(5,-7) on the y-axis.
As from the graph clearly we get the co-ordinates of the points M and N
Co-ordinate of the point M is (5,0)
Co-ordinate of the point N is (0,-7)
APPEARS IN
RELATED QUESTIONS
Find the values of x and y if:
(x - 1, y + 3) = (4, 4)
Find the values of x and y if:
(5x - 3y, y - 3x) = (4, -4)
State, true or false:
The origin (0, 0) lies on the x-axis.
State, true or false:
The point (a, b) lies on the y-axis if b = 0.
In the following, find the coordinates of the point whose abscissa is the solution of the first equation and ordinate is the solution of the second equation:
3 - 2x = 7; 2y + 1 = 10 - 2`(1)/(2)`y.
In the following, find the co-ordinates of the point whose abscissa is the solution of the first equation and ordinate is the solution of the second equation:
`5x - (5 - x) = (1)/(2) (3 - x); 4 -3y = (4 + y)/(3)`
In rectangle OABC; point O is the origin, OA = 10 units along x-axis and AB = 8 units. Find the co-ordinates of vertices A, B and C.
Find the co-ordinates of points whose: Abscissa is 5 and ordinate is -1
Find the co-ordinates of points whose: Abscissa is -4 and ordinate is -7
In each of the following, find the coordinates of the point whose abscissa is the solution of the first equation and ordinate is the solution of the second equation.
5 + 2x = `9: 3(1)/(2)y + 1` = 12 - 3y
