Advertisements
Advertisements
Question
Red queens and black jacks are removed from a pack of 52 playing cards. A card is drawn at random from the remaining cards, after reshuffling them. Find the probability that the card drawn is a king
Solution
In a pack of 52 playing cards, there are 2 red queens and 2 black jacks.
Red queens and black jacks are removed from the pack. Then,
Number of remaining cards = 52 − 4 = 48
∴ Total number of outcomes = 48
There are 4 king cards in the remaining pack of cards.
So, the favourable number of outcomes are 4.
∴ P(drawing a king) = \[\frac{\text{ Favourable number of outcomes }}{\text{ Total number of outcomes }} = \frac{4}{48} = \frac{1}{12}\]
APPEARS IN
RELATED QUESTIONS
In a certain race, there are three boys A, B, C. The winning probability of A is twice than B and the winning probability of B is twice than C. If P(A) + P(B) + P(C) = 1, then find the probability of win for each boy.
Two coins are tossed simultaneously. Write the sample space (S), n(S), the following event A
using set notation and n(A), where ‘A is the event of getting at least one head.’
Two dice are thrown. Find the probability of getting :
1) The sum of the numbers on their upper faces is at least 9.
2) The sum of the numbers on their upper faces is 15.
3) The number on the upper face of the second die is greater than the number on the upper face of the first die.
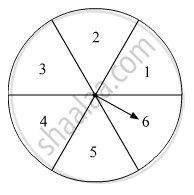
In fig. 7 is shown a disc on which a player spins an arrow twice. The fraction `a/b` is formed, where 'a' is the number of sector on which arrow stops on the first spin and 'b' is the number of the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction `a/b>1.`
A box contains cards bearing numbers from 6 to 70. If one card is drawn at random from the box, find the probability that it bears
(i) a one digit number.
(ii) a number divisible by 5.
(iii) an odd number less than 30.
(iv) a composite number between 50 and 70.
Two different coins are tossed simultaneously. The probability of getting at least one head is
(A)`1/2`
(B)`1/8`
(C)`3/4`
(D)`7/8`
The following table shows the blood-groups of employees in a bank.
Event C is : ‘the blood-group of an employee is AB.’
| Blood - group | A | B | AB | 0 |
| No. of employees | 20 | 40 | 15 | 25 |
If an employee is chosen at random, what is the probability that his blood-group is AB ?
Fill in the following boxes and find the answer
n(S)= ______
n(C)= ______
p(C)=________=_________
A piggy bank contains hundred 50 paise coins, fifity ₹1 coins, twenty ₹2 coins and ten ₹5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, find the probability that the coin which fell will be of value more than ₹1
One card is drawn from a well shuffled deck of 52 playing cards. What is the probability of getting a non-face card?
If \[\bar{E}\] denote the complement or negation of an even E, what is the value of P(E) + P(\[\bar{E}\]) ?
One card is drawn at random from a well shuffled deck of 52 cards. What is the probability of getting an ace?
A number is selected from numbers 1 to 25. The probability that it is prime is
Which of the following cannot be the probability of occurence of an event?
A two digit number is to be formed using the digits 0, 1, 2, 3. Repetition of the digits is allowed. Find the probability that a number so formed is a prime number.
A card is drawn from a well-shuffled pack of 52 cards. Find the probability of getting a black king.
Cards numbered 1 to 30 are put in a bag. A card is drawn at random from the bag. Find the probability that the number on the drawn card is not divisible by 3,
Once card is drawn at random from a well-shuffled deck of 52 cards. What is the probability of getting a black face card?
A die is thrown, find the probability of getting:
a number not greater than 4.
From 10 identical cards, numbered 1, 2, 3, ……, 10, one card is drawn at random. Find the probability that the number on the card drawn is a multiple of
2 and 3
Two dice are rolled, find the probability that the sum is equal to 4

