Advertisements
Advertisements
Question
∆RST मध्ये, ∠S = 90°, ∠T = 30°, RT = 12 सेमी, तर RS काढा.
Solution
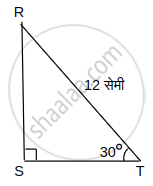
ΔRST मध्ये,
∠S = 90°, ∠T = 30°
∴ ∠R = 60° ..................(उरलेल्या कोनाचे माप)
∴ ΔRST 30° - 60° - 90° मापाचा त्रिकोण आहे.
∴ RS = `1/2 xx "RT"` ..........(30° कोनासमोरील बाजू)
= `1/2 xx 12`
RS = 6 सेमी
APPEARS IN
RELATED QUESTIONS
आकृती मधील ΔPSR मध्ये दिलेल्या माहितीवरून RP आणि PS काढा.
एका समभुज त्रिकोणाची बाजू 2a आहे, तर त्याची उंची काढा.
ΔABC हा समभुज त्रिकोण आहे. पाया BC वर P बिंदू असा आहे की PC = `1/ 3` BC, जर AB = 6 सेमी तर AP काढा.
सोबतच्या आकृतीत, ∆ABC मध्ये, AB ⊥ BC, AB = BC, तर ∠A चे माप किती?
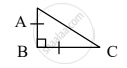
सोबतच्या आकृतीत, ∆ABC मध्ये, AB = BC, AC = `2sqrt2`, ∠ABC = 90°. तर AB ची लांबी किती?

4 सेमी बाजू असलेल्या समभुज त्रिकोणाची उंची किती?
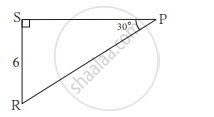
बाजूच्या आकृतीवरून जर AQ = 8 सेमी, तर AB ची लांबी काढा.
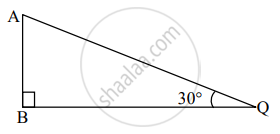
सोबतच्या आकृतीवरून, जर AC = 12 सेमी, तर AB ची लांबी काढण्यासाठी खालील कृती पूर्ण करा.
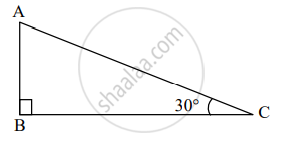
कृती: सोबतच्या आकृतीत, ∆ABC मध्ये, ∠ABC = 90°, ∠ACB = 30° यावरून,
∠BAC = `square`
म्हणजेच, ∆ABC हा 30° – 60° – 90° त्रिकोण आहे.
∆ABC मध्ये 30° – 60° – 90° त्रिकोणाच्या प्रमेयानुसार,
AB = `1/2"AC"` व `square` = `sqrt3/2"AC"`.
∴ `square` = `1/2 xx 12` व BC = `sqrt3/2 xx 12`
∴ `square` = 6 व BC = `6sqrt3.`
सोबतच्या आकृतीत, ∆ABC मध्ये, ∠ABC = 90°, ∠CAB = 30° AC = 14, तर AB व BC काढण्यासाठी खालील कृती पूर्ण करा.
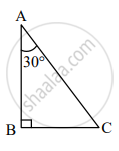
कृती: ∆ABC मध्ये, ∠ABC = 90°, ∠CAB = 30° यावरून, ∠BCA = `square`
30° – 60° – 90° त्रिकोणाच्या प्रमेयानुसार,
`square = 1/2 "AC" व square = sqrt3/2 "AC"`.
∴ BC = `1/2 xx square` व AB = `sqrt3/2 xx 14`
BC = 7 व AB = `7sqrt3`.
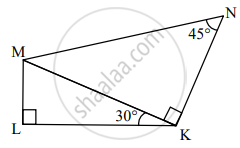
सोबतच्या आकृतीत, LK = `6sqrt2` तर MK, ML, MN काढा.