Advertisements
Advertisements
Question
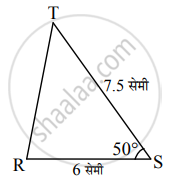
ΔRST ∼ ΔUAY, ΔRST मध्ये, RS = 6 सेमी, ∠S = 50°, ST = 7.5 सेमी. त्रिकोणाच्या संगत बाजूंचे गुणोत्तर 5.4 असल्यास ΔUAY काढा.
Solution
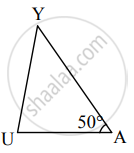
कच्ची आकृती
ΔRST ∼ ΔUAY
∴ ∠S = ∠A = 50° .............[समरूप त्रिकोणांचे संगत कोन]
∴ `"RS"/"UA" = "ST"/"AY" = "RT"/"UY"` ......(i) [समरूप त्रिकोणांच्या संगत बाजू]
संगत बाजूंचे गुणोत्तर 5:4 असल्यामुळे,
∴ `"RS"/"UA" = "ST"/"AY" = "RT"/"UY" = 5/4` ....[(i) वरून]
∴ `6/"UA" = 7.5/"AY" = 5/4` .......…(ii)
आता, `6/"UA" = 5/4` ..........[(ii) वरून]
∴ 5 × UA = 6 × 4
∴ UA = `(6 xx 4)/5`
∴ UA = 4.8 सेमी
आता, `7.5/"AY" = 5/4` .........[(ii) वरून]
∴ AY × 5 = 7.5 × 4
∴ AY = `(7.5 xx 4)/5`
∴ AY = 6 सेमी
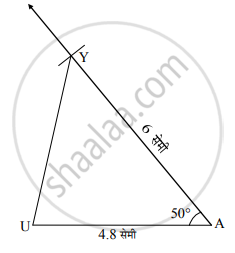
∴ ΔUAY मध्ये, UA = 4.8 सेमी, AY = 6 सेमी व ∠A = 50°
APPEARS IN
RELATED QUESTIONS
ΔPQR ~ ΔLTR, ΔPQR मध्ये PQ = 4.2 सेमी, QR = 5.4 सेमी, PR = 4.8 सेमी आणि `"PQ"/"LT"` = `3/4` तर ΔPQR व ΔLTR काढा.
ΔRST ~ ΔXYZ, ΔRST मध्ये RS = 4.5 सेमी, ∠RST = 40°, ST = 5.7 सेमी आणि `"RS"/"XY" = 3/5` तर ΔRST व ΔXYZ काढा.
ΔAMT ~ ΔAHE, ΔAMT मध्ये AM = 6.3 सेमी, ∠TAM = 50°, AT = 5.6 सेमी आणि `"AM"/"AH" = 7/5` तर ΔAHE काढा.
जर ΔABC ~ ΔLBN, ΔABC मध्ये AB= 5.1 सेमी, ∠B = 40°, BC = 4.8 सेमी, `"AC"/"LN" = 4/7` तर ΔABC व ΔLBN काढा.
ΔPYQ असा काढा की, PY = 6.3 सेमी, YQ = 7.2 सेमी, PQ = 5.8 सेमी. ΔXYZ हा ΔPYQ शी समरूप त्रिकोण असा काढा की, `"YZ"/"YQ" = 6/5`.
ΔABC हा 60° काढा व तो दुभागा.
ΔABC ∼ ΔLMN, ΔABC मध्ये, AB = 5.5 सेमी, BC = 6 सेमी, CA = 5.5 सेमी, MN = 4.8 सेमी, तर ΔABC व ΔLMN काढा.
ΔSHR ∼ ΔSVU, ΔSHR मध्ये SH = 4.5 सेमी, HR = 5.2 सेमी, SR = 5.8 सेमी, `"HS"/"SV" = 3/5`, तर ΔSVU काढा.
ΔABC मध्ये, BC = 6 सेमी, ∠B = 45°, ∠A = 100°. ΔABC ∼ ΔPBQ. त्रिकोणाच्या संगत बाजूंचे गुणोत्तर 7:4 असल्यास ΔABC व ΔPBQ काढा.
ΔPQR मध्ये, ∠P = 40°, PQ ≅ PR, QR = 7 सेमी. ΔXYZ ∼ ΔPQR, XY:PQ = 3:2 असल्यास ΔXYZ काढा.
