Advertisements
Advertisements
Question
Show on a graph the variation of the de Broglie wavelength (λ) associated with an electron, with the square root of accelerating potential (V) ?
Solution
`lambda = 1.22/sqrtV`
`therefore lambda sqrtV=` const
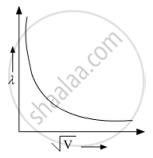
Hence, we get a hyperbola.
RELATED QUESTIONS
Plot a graph showing variation of de Broglie wavelength λ versus `1/sqrtV` , where V is accelerating potential for two particles A and B, carrying the same charge but different masses m1, m2 (m1 > m2). Which one of the two represents a particle of smaller mass and why?
A proton and an α -particle are accelerated through the same potential difference. Which one of the two has greater de-Broglie wavelength Justify your answer.
An electron is accelerated from rest through a potential V. Obtain the expression for the de-Broglie wavelength associated with it ?
A proton and an electron have same kinetic. Which one has greater de-Broglie wavelength and why?
Consider the de-Broglie wavelength of an electron and a proton. Which wavelength is smaller if the two particles have (a) the same speed (b) the same momentum (c) the same energy?
Let p and E denote the linear momentum and energy of a photon. If the wavelength is decreased,
A running man has half the kinetic energy of that of a boy of half of his mass. The man speeds up by 1 m/s so as to have the same K.E. as that of the boy. The original speed of the man will be:
The de- Broglie wave length of an electron moving with a speed of 6.6 × 105 m/s is approximately
Find the de-Broglie Wavelength for an electron moving at the speed of 5.0 × 106 m/s. (mass of electron is 9.1 × 10-31)
An oil drop carrying a charge q has a mass m kg it is falling freely in air with terminal speed v. the electron field required to make the drop move upward with the same speed is
