Advertisements
Advertisements
Question
Solve the following :
Find the area of the region bounded by the straight line 2y = 5x + 7, X-axis and x = 2, x = 5.
Solution
The equation of the line is 2y = 5x + 7,
i.e. y = `(5)/(2)x + (7)/(2)`
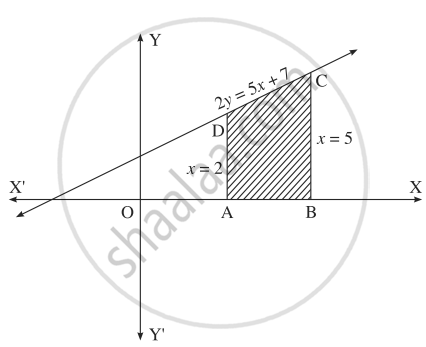
Required area = area of the region ABCDA
= area under the line y = `(5)/(2)x + (7)/(2)` between x = 2 and x = 5
= `int_2^5 (5/2x + 7/2)*dx`
= `(5)/(2)* int_2^5x*dx + (7)/(2) int_2^5 1*dx`
= `(5)/(2)[x^2/2]_2^5 + (7)/(2)[x]_2^5`
= `(5)/(2)[25/2 - 4/2] + (7)/(2)[5 - 2]`
= `(5)/(2) xx (21)/(2) + (21)/(2)`
= `(105)/(4) + (42)/(4)`
= `(147)/(4)"sq units"`.
APPEARS IN
RELATED QUESTIONS
Find the area of the region bounded by the following curves, X-axis and the given lines : y = sin x, x = 0, x = `pi/(2)`
Find the area of the region bounded by the following curves, X-axis and the given lines : x = 0, x = 5, y = 0, y = 4
Find the area of the region bounded by the following curves, X-axis and the given lines: y2 = 16x, x = 0, x = 4
Find the area of the region included between y2 = 2x and y = 2x.
Find the area of the region included between: y2 = 4x, and y = x
Find the area of the region included between: y = x2 and the line y = 4x
Find the area of the region included between y = x2 + 3 and the line y = x + 3.
Choose the correct option from the given alternatives :
The area of the region enclosed by the curve y = `(1)/x`, and the lines x = e, x = e2 is given by
Choose the correct option from the given alternatives :
The area bounded by the curve y = x3, the X-axis and the lines x = – 2 and x = 1 is
The area of the region bounded by y = cos x, Y-axis and the lines x = 0, x = 2π is ______.
Choose the correct option from the given alternatives :
The area bounded by the parabola y2 = 8x, the X-axis and the latus rectum is
Choose the correct option from the given alternatives :
The area of the circle x2 + y2 = 25 in first quadrant is
Choose the correct option from the given alternatives :
The area bounded by the ellipse `x^2/a^2 y^2/b^2` = 1 and the line `x/a + y/b` = 1 is
The area bounded by the curve y = tan x, X-axis and the line x = `pi/(4)` is ______.
Choose the correct option from the given alternatives :
The area of the region included between the line x + y = 1 and the circle x2 + y2 = 1 is
Solve the following :
Find the area of the region bounded by the following curve, the X-axis and the given lines : 0 ≤ x ≤ 5, 0 ≤ y ≤ 2
Solve the following :
Find the area of the region bounded by the curve (y – 1)2 = 4(x + 1) and the line y = (x – 1).
The area of the region bounded by the ellipse x2/64 + y2/100 = 1, is ______ sq.units
The area bounded by the parabola y2 = x along the X-axis and the lines x = 0, x = 2 is ______ sq.units
The area bounded by the curve y2 = x2, and the line x = 8 is ______
The area bounded by the parabola y2 = 32x the X-axis and the latus rectum is ______ sq.units
The area enclosed by the line 2x + 3y = 6 along X-axis and the lines x = 0, x = 3 is ______ sq.units
Find the area bounded by the curve y2 = 36x, the line x = 2 in first quadrant
Find the area of the region bounded by the curve y2 = 8x, the X−axis and the given lines x = 1, x = 3, y ≥ 0
Find the area of the region bounded by the curve x2 = 12y, the Y−axis and the given lines y = 2, y = 4, x ≥ 0
Using integration, find the area of the region bounded by the line 2y + x = 8 , X−axis and the lines x = 2 and x = 4
Find the area of the region bounded by the curves x2 = 8y, y = 2, y = 4 and the Y-axis, lying in the first quadrant
Find the area of the region bounded by the curves y2 = 4ax and x2 = 4ay
Find the area of the region bounded by the curve y = x2 and the line y = 4.
Find the area common to the parabola y2 = x – 3 and the line x = 5.
Find the area of the region bounded by the curve y = x2, and the lines x = 1, x = 2, and y = 0.
