Advertisements
Advertisements
Question
Solve the following pair of equations:
`(2xy)/(x + y) = 3/2, (xy)/(2x - y) = (-3)/10, x + y ≠ 0, 2x - y ≠ 0`
Solution
Given pair of equations is
`(2xy)/(x + y) = 3/2`, where x + y ≠ 0
⇒ `(x + y)/(2xy) = 2/3`
⇒ `x/(xy) + y/(xy) = 4/3`
⇒ `1/y + 1/x = 4/3` .....(i)
And `(xy)/(2x - y) = (-3)/10`, where 2x – y ≠ 0
⇒ `(2x - y)/(xy) = (-10)/3`
⇒ `(2x)/(xy) - y/(xy) = (-10)/3`
⇒ `2/y - 1/x = (-10)/3` .....(ii)
Now, put `1/x` = u and `1/y` = v, then the pair of equations becomes
v + u = `4/3` .....(iii)
And 2v – u = `(-10)/3` .....(iv)
On adding both equations, we get
3v = `4/3 - 10/3`
= `(-6)/3`
⇒ 3v = – 2
⇒ v = `(-2)/3`
Now, put the value of v in equation (iii), we get
`(-2)/3 + u = 4/3`
⇒ u = `4/3 + 2/3`
= `6/3`
= 2
∴ x = `1/u = 1/2`
And y = `1/v`
= `1/((-2)/3)`
= `(-3)/2`
Hence, the required values of x and y are `1/2` and `(-3)/2`, respectively.
APPEARS IN
RELATED QUESTIONS
Solve the following system of equations by cross-multiplication method x + y = a – b; ax – by = a2 + b2
Solve the following system of equations by the method of cross-multiplication. `\frac{a}{x}-\frac{b}{y}=0;\text{}\frac{ab^{2}}{x}+\frac{a^{2}b}{y}=a^{2}+b^{2};` Where x ≠ 0, y ≠ 0
Solve the following systems of equations:
`1/(2x) + 1/(3y) = 2`
`1/(3x) + 1/(2y) = 13/6`
Solve the following systems of equations:
`(7x - 2y)/"xy" = 5`
`(8x + 7y)/"xy" = 15`
Solve each of the following systems of equations by the method of cross-multiplication :
(a + 2b)x + (2a − b)y = 2
(a − 2b)x + (2a + b)y = 3
Solve each of the following systems of equations by the method of cross-multiplication :
2(ax – by) + a + 4b = 0
2(bx + ay) + b – 4a = 0
Solve the system of equations by using the method of cross multiplication:
6x - 5y - 16 = 0,
7x - 13y + 10 = 0
Solve the system of equation by using the method of cross multiplication:
`5/("x+y") - 2/("x− y") + 1 = 0, 15/("x+y") + 7/("x− y") – 10 = 0`
Find the values of x and y in the following rectangle [see figure].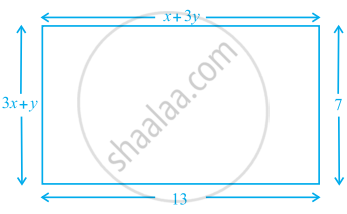
A railway half ticket costs half the full fare, but the reservation charges are the same on a half ticket as on a full ticket. One reserved first class ticket from the station A to B costs Rs 2530. Also, one reserved first class ticket and one reserved first class half ticket from A to B costs Rs 3810. Find the full first class fare from station A to B, and also the reservation charges for a ticket.
