Advertisements
Advertisements
Question
State whether the following statement is True or False:
The maximum value of Z = 5x + 3y subjected to constraints 3x + y ≤ 12, 2x + 3y ≤ 18, 0 ≤ x, y is 20
Options
True
False
Solution
False
APPEARS IN
RELATED QUESTIONS
A company produces two types of goods A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of golds while that of type B requires 1 g of silver and 2 g of gold. The company can procure a maximum of 9 g of silver and 8 g of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, formulate LPP to maximize profit.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Solve the following L.P.P. by graphical method:
Minimize: Z = 6x + 2y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
Choose the correct alternative :
The point at which the maximum value of z = x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x ≥ 0, y ≥ 0 is
The constraint that a factory has to employ more women (y) than men (x) is given by _______
Solve the following problem :
Maximize Z = 5x1 + 6x2 Subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x ≥ 0, x2 ≥ 0
Solve the following problem :
Minimize Z = 4x + 2y Subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0, y ≥ 0
Solve the following problem :
Maximize Z = 4x1 + 3x2 Subject to 3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0
Solve the following problem :
A factory produced two types of chemicals A and B The following table gives the units of ingredients P & Q (per kg) of Chemicals A and B as well as minimum requirements of P and Q and also cost per kg. of chemicals A and B.
| Ingredients per kg. /Chemical Units | A (x) |
B (y) |
Minimum requirements in |
| P | 1 | 2 | 80 |
| Q | 3 | 1 | 75 |
| Cost (in ₹) | 4 | 6 |
Find the number of units of chemicals A and B should be produced so as to minimize the cost.
Choose the correct alternative:
The point at which the minimum value of Z = 8x + 12y subject to the constraints 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0 is obtained at the point
Choose the correct alternative:
The corner points of the feasible region are (0, 3), (3, 0), (8, 0), `(12/5, 38/5)` and (0, 10), then the point of maximum Z = 6x + 4y = 48 is at
Choose the correct alternative:
The corner points of the feasible region are (4, 2), (5, 0), (4, 1) and (6, 0), then the point of minimum Z = 3.5x + 2y = 16 is at
State whether the following statement is True or False:
The graphical solution set of the inequations 0 ≤ y, x ≥ 0 lies in second quadrant
Maximize Z = 400x + 500y subject to constraints
x + 2y ≤ 80, 2x + y ≤ 90, x ≥ 0, y ≥ 0
Solve the following LPP graphically:
Maximize Z = 9x + 13y subject to constraints
2x + 3y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequation | Equation | X intercept | Y intercept | Region |
| 2x + 3y ≤ 18 | 2x + 3y = 18 | (9, 0) | (0, ___) | Towards origin |
| 2x + y ≤ 10 | 2x + y = 10 | ( ___, 0) | (0, 10) | Towards origin |
| x ≥ 0, y ≥ 0 | x = 0, y = 0 | X axis | Y axis | ______ |
The feasible region is OAPC, where O(0, 0), A(0, 6),
P( ___, ___ ), C(5, 0)
The optimal solution is in the following table:
| Point | Coordinates | Z = 9x + 13y | Values | Remark |
| O | (0, 0) | 9(0) + 13(0) | 0 | |
| A | (0, 6) | 9(0) + 13(6) | ______ | |
| P | ( ___,___ ) | 9( ___ ) + 13( ___ ) | ______ | ______ |
| C | (5, 0) | 9(5) + 13(0) | ______ |
∴ Z is maximum at __( ___, ___ ) with the value ___.
Solve the LPP graphically:
Minimize Z = 4x + 5y
Subject to the constraints 5x + y ≥ 10, x + y ≥ 6, x + 4y ≥ 12, x, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequations | Equations | X intercept | Y intercept | Region |
| 5x + y ≥ 10 | 5x + y = 10 | ( ___, 0) | (0, 10) | Away from origin |
| x + y ≥ 6 | x + y = 6 | (6, 0) | (0, ___ ) | Away from origin |
| x + 4y ≥ 12 | x + 4y = 12 | (12, 0) | (0, 3) | Away from origin |
| x, y ≥ 0 | x = 0, y = 0 | x = 0 | y = 0 | 1st quadrant |
∵ Origin has not satisfied the inequations.
∴ Solution of the inequations is away from origin.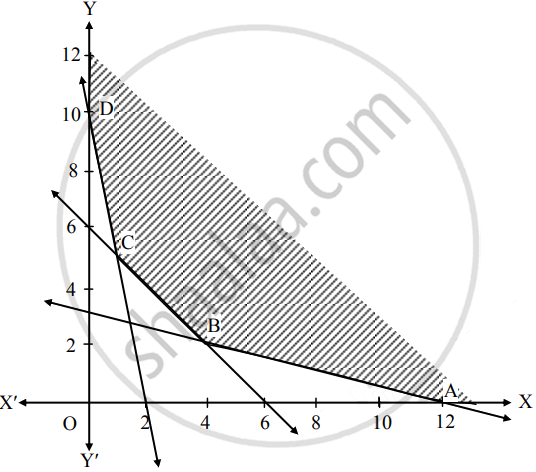
The feasible region is unbounded area which is satisfied by all constraints.
In the figure, ABCD represents
The set of the feasible solution where
A(12, 0), B( ___, ___ ), C ( ___, ___ ) and D(0, 10).
The coordinates of B are obtained by solving equations
x + 4y = 12 and x + y = 6
The coordinates of C are obtained by solving equations
5x + y = 10 and x + y = 6
Hence the optimum solution lies at the extreme points.
The optimal solution is in the following table:
| Point | Coordinates | Z = 4x + 5y | Values | Remark |
| A | (12, 0) | 4(12) + 5(0) | 48 | |
| B | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | ______ |
| C | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | |
| D | (0, 10) | 4(0) + 5(10) | 50 |
∴ Z is minimum at ___ ( ___, ___ ) with the value ___
If z = 200x + 500y .....(i)
Subject to the constraints:
x + 2y ≥ 10 .......(ii)
3x + 4y ≤ 24 ......(iii)
x, 0, y ≥ 0 ......(iv)
At which point minimum value of Z is attained.
Shraddho wants to invest at most ₹ 25,000/- in saving certificates and fixed deposits. She wants to invest at least ₹ 10,000/- in saving certificate and at least ₹ 15,000/- in fixed deposits. The rate of interest on saving certificate is 5% and that on fixed deposits is 7% per annum. Formulate the above problem as LPP to determine maximum income yearly.
