Advertisements
Advertisements
Question
Solve the following problem :
Minimize Z = 4x + 2y Subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0, y ≥ 0
Solution
To find the graphical solution, construct the table as follows:
| Inequation | equation | Double intercept form | Points (x1, x2) | Points (x1, x2) |
| 3x + y ≥ 27 | 3x + y = 27 | `x/(9) + y/(27)` = 1 | A (9, 0) B (0, 27) |
3(0) + 0 ≥ 27 |
| x + y ≥ 21 | x + y = 21 | `x/(21) + y/(21)` = 1 | C (21, 0) D (0, 21) |
(0) + 0 ≥ 21 ∴ 0 ≥ 21 ∴ non-origin-side |
| x ≥ 0 | x = 0 | – | R.H.S. of Y-axis | |
| y ≥ 0 | y = 0 | above X-axis |
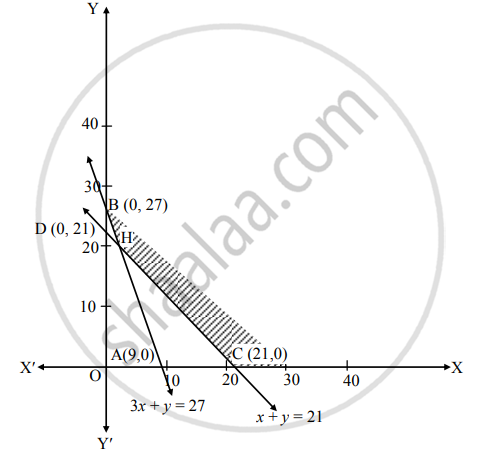
The shaded portion CHB is the feasible region.
Whose vertices are C(21, 0), H and B(0, 27)
H is the point of intersection of lines
3x + y = 27 …(i)
x + y = 21 …(ii)
∴ By (i) – (ii), we get
3 x + y = 27
x + y = 21
– – –
2x = 6
∴ x = `(6)/(2)` = 3
Substituting x = 3 in (ii), we get
3 + y = 21
∴ y = 18
∴ H (3, 18)
Here, the objective function is Z = 4x + 2y
Now, we will find minimum value of Z as follows:
| Feasible points | The value of Z = 4x + 2y |
| C (21, 0) | Z = 4(21) + 2(0) = 84 |
| H (3, 18) | Z = 4(3) + 2(18) = 12 + 36 = 48 |
| B (0, 27) | Z = 4(0) + 2(27) = 54 |
∴ Z has minimum value 48 at H (3, 18)
∴ Z is minimum, when x = 3, y = 18
APPEARS IN
RELATED QUESTIONS
A company produces two types of goods A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of golds while that of type B requires 1 g of silver and 2 g of gold. The company can procure a maximum of 9 g of silver and 8 g of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, formulate LPP to maximize profit.
Amit's mathematics teacher has given him three very long lists of problems with the instruction to submit not more than 100 of them (correctly solved) for credit. The problem in the first set are worth 5 points each, those in the second set are worth 4 points each, and those in the third set are worth 6 points each. Amit knows from experience that he requires on the average 3 minutes to solve a 5 point problem, 2 minutes to solve a 4 point problem, and 4 minutes to solve a 6 point problem. Because he has other subjects to worry about, he can not afford to devote more than
Solve the following L.P.P. by graphical method :
Maximize : Z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solve the following L.P.P. by graphical method:
Minimize: Z = 6x + 2y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Choose the correct alternative :
The maximum value of z = 5x + 3y. subject to the constraints
The region represented by the inequality y ≤ 0 lies in _______ quadrants.
Graphical solution set of x ≤ 0, y ≥ 0 in xy system lies in second quadrant.
Solve the following problem :
Maximize Z = 5x1 + 6x2 Subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x ≥ 0, x2 ≥ 0
Solve the following problem :
Minimize Z = 2x + 3y Subject to x – y ≤ 1, x + y ≥ 3, x ≥ 0, y ≥ 0
Solve the following problem :
Maximize Z = 4x1 + 3x2 Subject to 3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x1 ≥ 0, x2 ≥ 0
Choose the correct alternative:
The point at which the minimum value of Z = 8x + 12y subject to the constraints 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0 is obtained at the point
Choose the correct alternative:
The corner points of the feasible region are (4, 2), (5, 0), (4, 1) and (6, 0), then the point of minimum Z = 3.5x + 2y = 16 is at
State whether the following statement is True or False:
A convex set includes the points but not the segment joining the points
State whether the following statement is True or False:
The graphical solution set of the inequations 0 ≤ y, x ≥ 0 lies in second quadrant
A company manufactures two types of ladies dresses C and D. The raw material and labour available per day is given in the table.
| Resources | Dress C(x) | Dress D(y) | Max. availability |
| Raw material | 5 | 4 | 60 |
| Labour | 5 | 3 | 50 |
P is the profit, if P = 50x + 100y, solve this LPP to find x and y to get the maximum profit
Smita is a diet conscious house wife, wishes to ensure certain minimum intake of vitamins A, B and C for the family. The minimum daily needs of vitamins A, B, and C for the family are 30, 20, and 16 units respectively. For the supply of the minimum vitamin requirements Smita relies on 2 types of foods F1 and F2. F1 provides 7, 5 and 2 units of A, B, C vitamins per 10 grams and F2 provides 2, 4 and 8 units of A, B and C vitamins per 10 grams. F1 costs ₹ 3 and F2 costs ₹ 2 per 10 grams. How many grams of each F1 and F2 should buy every day to keep her food bill minimum
A wholesale dealer deals in two kinds of mixtures A and B of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew and 180 grams of hazel nuts. A dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew and 540 grams of hazel nuts. Mixture A costs ₹ 8 and B costs ₹ 12 per kg. How many kgs of each mixture should he use to minimize the cost of the kgs
Minimize Z = 24x + 40y subject to constraints
6x + 8y ≥ 96, 7x + 12y ≥ 168, x ≥ 0, y ≥ 0
Shraddho wants to invest at most ₹ 25,000/- in saving certificates and fixed deposits. She wants to invest at least ₹ 10,000/- in saving certificate and at least ₹ 15,000/- in fixed deposits. The rate of interest on saving certificate is 5% and that on fixed deposits is 7% per annum. Formulate the above problem as LPP to determine maximum income yearly.
Graphical solution set of the inequations x ≥ 0 and y ≤ 0 lies in ______ quadrant.
