Advertisements
Advertisements
Question
Suggest optimum solution to the following assignment. Problem, also find the total minimum service time.
Service Time ( in hrs.)
| Counters | Salesmen | |||
| A | B | C | D | |
| W | 41 | 72 | 39 | 52 |
| X | 22 | 29 | 49 | 65 |
| Y | 27 | 39 | 60 | 51 |
| Z | 45 | 50 | 48 | 52 |
Solution
This problem is already 4 x 4.
Select the smallest element in each row and subtract it from every element in each row :
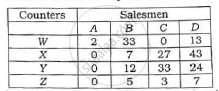
Select the smallest element in each column of the above matrix and subtract it form every element in that column.
Draw the minimum lines covering all zeros.
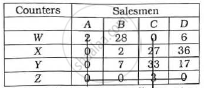
Minimum lines covering all zeros is not equal to the order of the matrix.
Minimum uncovered value 2 is subtracted from uncovered values and added to values at intersection of the lines.
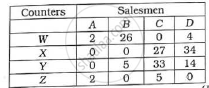
Draw minimum lines covering all the zeros.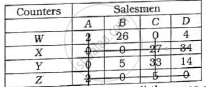
Minimum lines covering all the zeros equal to the order of the matrix.
∴ Allocation of counters can be done.
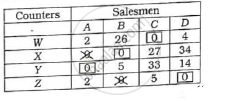
The allocation of the counters to the salesmen is
W → C, X → B, Y → A, Z → D
The minimum time = 39 + 29 + 27 +52 = 147 Hrs.
APPEARS IN
RELATED QUESTIONS
Solve the following minimal assignment problem and hence find the minimum value :
| I | II | III | IV | |
| A | 2 | 10 | 9 | 7 |
| B | 13 | 2 | 12 | 2 |
| C | 3 | 4 | 6 | 1 |
| D | 4 | 15 | 4 | 9 |
Solve the following minimal assignment problem :
| Machines | A | B | C | D | E |
| M1 | 27 | 18 | ∞ | 20 | 21 |
| M2 | 31 | 24 | 21 | 12 | 17 |
| M3 | 20 | 17 | 20 | ∞ | 16 |
| M4 | 21 | 28 | 20 | 16 | 27 |
Determine `l_92 and l_93, "given that" l_91 = 97, d_91 = 38 and q_92 = 27/59`
Solve the following minimal assignment problem and hence find minimum time where '- ' indicates that job cannot be assigned to the machine :
| Machines | Processing time in hours | ||||
| A | B | C | D | E | |
| M1 | 9 | 11 | 15 | 10 | 11 |
| M2 | 12 | 9 | - | 10 | 9 |
| M3 | - | 11 | 14 | 11 | 7 |
| M4 | 14 | 8 | 12 | 7 | 8 |
Solve the following maximal assignment problem :
| Branch Manager | Monthly Business ( Rs. lakh) | |||
| A | B | C | D | |
| P | 11 | 11 | 9 | 9 |
| Q | 13 | 16 | 11 | 10 |
| R | 12 | 17 | 13 | 8 |
| S | 16 | 14 | 16 | 12 |
In a factory there are six jobs to be performed each of which should go through two machines A and B in the order A - B. The processing timing (in hours) for the jobs arc given here. You are required to determine the sequence for performing the jobs that would minimize the total elapsed time T. What is the value of T? Also find the idle time for machines · A and B.
| Jobs | J1 | J2 | J3 | J4 | J5 | J6 |
| Machine A | 1 | 3 | 8 | 5 | 6 | 3 |
| MAchine B | 5 | 6 | 3 | 2 | 2 | 10 |
A job production unit has four jobs A, B, C, D which can be manufactured on each of the four machines P, Q, R and S. The processing cost of each job for each machine is given in the following table:
| Jobs | Machines (Processing Cost in ₹) |
|||
| P | Q | R | S | |
| A | 31 | 25 | 33 | 29 |
| B | 25 | 24 | 23 | 21 |
| C | 19 | 21 | 23 | 24 |
| D | 38 | 36 | 34 | 40 |
Find the optimal assignment to minimize the total processing cost.
Five different machines can do any of the five required jobs, with different profits resulting from each assignment as shown below:
| Job | Machines (Profit in ₹) | ||||
| A | B | C | D | E | |
| 1 | 30 | 37 | 40 | 28 | 40 |
| 2 | 40 | 24 | 27 | 21 | 36 |
| 3 | 40 | 32 | 33 | 30 | 35 |
| 4 | 25 | 38 | 40 | 36 | 36 |
| 5 | 29 | 62 | 41 | 34 | 39 |
Find the optimal assignment schedule.
The assignment problem is said to be unbalance if ______
The assignment problem is said to be balanced if ______.
Choose the correct alternative :
The assignment problem is said to be balanced if it is a ______.
Choose the correct alternative :
In an assignment problem if number of rows is greater than number of columns then
The objective of an assignment problem is to assign ______.
Fill in the blank :
When an assignment problem has more than one solution, then it is _______ optimal solution.
In an assignment problem, if number of column is greater than number of rows, then a dummy column is added.
State whether the following is True or False :
In assignment problem, each facility is capable of performing each task.
Solve the following problem :
A plant manager has four subordinates, and four tasks to be performed. The subordinates differ in efficiency and the tasks differ in their intrinsic difficulty. This estimate of the time each man would take to perform each task is given in the effectiveness matrix below.
| I | II | III | IV | |
| A | 7 | 25 | 26 | 10 |
| B | 12 | 27 | 3 | 25 |
| C | 37 | 18 | 17 | 14 |
| D | 18 | 25 | 23 | 9 |
How should the tasks be allocated, one to a man, as to minimize the total man hours?
Choose the correct alternative:
The assignment problem is said to be balanced if ______
In an assignment problem if number of rows is greater than number of columns, then dummy ______ is added
State whether the following statement is True or False:
In assignment problem, if number of columns is greater than number of rows, then a dummy row is added
State whether the following statement is True or False:
In assignment problem each worker or machine is assigned only one job
What is the Assignment problem?
Assign four trucks 1, 2, 3 and 4 to vacant spaces A, B, C, D, E and F so that distance travelled is minimized. The matrix below shows the distance.
| 1 | 2 | 3 | 4 | |
| A | 4 | 7 | 3 | 7 |
| B | 8 | 2 | 5 | 5 |
| C | 4 | 9 | 6 | 9 |
| D | 7 | 5 | 4 | 8 |
| E | 6 | 3 | 5 | 4 |
| F | 6 | 8 | 7 | 3 |
Choose the correct alternative:
If number of sources is not equal to number of destinations, the assignment problem is called ______
Choose the correct alternative:
In an assignment problem involving four workers and three jobs, total number of assignments possible are
A car hire company has one car at each of five depots a, b, c, d and e. A customer in each of the fine towers A, B, C, D and E requires a car. The distance (in miles) between the depots (origins) and the towers(destinations) where the customers are given in the following distance matrix.
| a | b | c | d | e | |
| A | 160 | 130 | 175 | 190 | 200 |
| B | 135 | 120 | 130 | 160 | 175 |
| C | 140 | 110 | 155 | 170 | 185 |
| D | 50 | 50 | 80 | 80 | 110 |
| E | 55 | 35 | 70 | 80 | 105 |
How should the cars be assigned to the customers so as to minimize the distance travelled?
A job production unit has four jobs P, Q, R, and S which can be manufactured on each of the four machines I, II, III, and IV. The processing cost of each job for each machine is given in the following table:
| Job | Machines (Processing cost in ₹) |
|||
| I | II | III | IV | |
| P | 31 | 25 | 33 | 29 |
| Q | 25 | 24 | 23 | 21 |
| R | 19 | 21 | 23 | 24 |
| S | 38 | 36 | 34 | 40 |
Find the optimal assignment to minimize the total processing cost.
Five wagons are available at stations 1, 2, 3, 4 and 5. These are required at 5 stations I, II, III, IV and V. The mileage between various stations are given in the table below. How should the wagons be transported so as to minimize the mileage covered?
| I | II | III | IV | V | |
| 1 | 10 | 5 | 9 | 18 | 11 |
| 2 | 13 | 9 | 6 | 12 | 14 |
| 3 | 7 | 2 | 4 | 4 | 5 |
| 4 | 18 | 9 | 12 | 17 | 15 |
| 5 | 11 | 6 | 14 | 19 | 10 |
A job production unit has four jobs P, Q, R, S which can be manufactured on each of the four machines I, II, III and IV. The processing cost of each job for each machine is given in the following table :
| Job | Machines (Processing cost in ₹) |
|||
| I | II | III | IV | |
| P | 31 | 25 | 33 | 29 |
| Q | 25 | 24 | 23 | 21 |
| R | 19 | 21 | 23 | 24 |
| S | 38 | 36 | 34 | 40 |
Complete the following activity to find the optimal assignment to minimize the total processing cost.
Solution:
Step 1: Subtract the smallest element in each row from every element of it. New assignment matrix is obtained as follows :
| Job | Machines (Processing cost in ₹) |
|||
| I | II | III | IV | |
| P | 6 | 0 | 8 | 4 |
| Q | 4 | 3 | 2 | 0 |
| R | 0 | 2 | 4 | 5 |
| S | 4 | 2 | 0 | 6 |
Step 2: Subtract the smallest element in each column from every element of it. New assignment matrix is obtained as above, because each column in it contains one zero.
Step 3: Draw minimum number of vertical and horizontal lines to cover all zeros:
| Job | Machines (Processing cost in ₹) |
|||
| I | II | III | IV | |
| P | 6 | 0 | 8 | 4 |
| Q | 4 | 3 | 2 | 0 |
| R | 0 | 2 | 4 | 5 |
| S | 4 | 2 | 0 | 6 |
Step 4: From step 3, as the minimum number of straight lines required to cover all zeros in the assignment matrix equals the number of rows/columns. Optimal solution has reached.
Examine the rows one by one starting with the first row with exactly one zero is found. Mark the zero by enclosing it in (`square`), indicating assignment of the job. Cross all the zeros in the same column. This step is shown in the following table :
| Job | Machines (Processing cost in ₹) |
|||
| I | II | III | IV | |
| P | 6 | 0 | 8 | 4 |
| Q | 4 | 3 | 2 | 0 |
| R | 0 | 2 | 4 | 5 |
| S | 4 | 2 | 0 | 6 |
Step 5: It is observed that all the zeros are assigned and each row and each column contains exactly one assignment. Hence, the optimal (minimum) assignment schedule is :
| Job | Machine | Min.cost |
| P | II | `square` |
| Q | `square` | 21 |
| R | I | `square` |
| S | III | 34 |
Hence, total (minimum) processing cost = 25 + 21 + 19 + 34 = ₹`square`
