Advertisements
Advertisements
Question
Suppose an attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2. Write down the dimensional formulae and appropriate SI units of C and k.
Solution
Given, nuclear force of attraction,
\[F = C\frac{e^{- Kr}}{r^2}\]
Here e−Kr is just a pure number, i.e. a dimensionless quantity. So,
\[\left[ C \right] = \left[ F \right] \times \left[ r^2 \right]\]
\[\left[ C \right] = \left[ {MLT}^{- 2} \right] \times \left[ L^2 \right]\]
\[\left[ C \right] = \left[ {ML}^3 T^{- 2} \right]\]
C = kg ⋅ m3 ⋅ s −2
\[\text{ And } \left[ K \right] = \frac{1}{\left[ r \right]} = \left[ L^{- 1} \right]\]
SI units: m−1
APPEARS IN
RELATED QUESTIONS
Check that the ratio ke2/G memp is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
Three-point charges q, – 4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q

(b) Find out the amount of the work done to separate the charges at infinite distance.
Write any two important points of similarities and differences each between Coulomb's law for the electrostatic field and Biot-Savart's law of the magnetic field ?
Plot a graph showing the variation of coulomb force (F) versus ,`(1/r^2)` where r is the distance between the two charges of each pair of charges: (1 μC, 2 μC) and (2 μC, − 3 μC). Interpret the graphs obtained.
Two charges 2.0 × 10−6 C and 1.0 × 10−6 C are placed at a separation of 10 cm. Where should a third charge be placed, such that it experiences no net force due to these charges?
A hydrogen atom contains one proton and one electron. It may be assumed that the electron revolves in a circle of radius 0.53 angstrom (1 angstrom = 10−10 m and is abbreviated as Å ) with the proton at the centre. The hydrogen atom is said to be in the ground state in this case. Find the magnitude of the electric force between the proton and the electron of a hydrogen atom in its ground state.
Two charged particles with charge 2.0 × 10−8 C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
A water particle of mass 10.0 mg and with a charge of 1.50 × 10−6 C stays suspended in a room. What is the magnitude of electric field in the room? What is its direction ?
Answer the following question.
What is relative permittivity?
Polarised dielectric is equivalent to ______.
The ratio of the forces between two small spheres with constant charge (a) in air (b) in a medium of dielectric constant K is ______.
Two identical thin rings, each of radius a meter, are coaxially placed at a distance R meter apart. If Q1 coulomb and Q2 coulomb are respectively the charges uniformly spread on the two rings, the work done in moving a charge q coulomb from the centre of one ring to that of the other is ______.
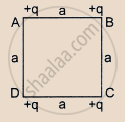
Four equal charges q are placed at the four comers A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be ______.
Two charge – 10c and + 10 c are placed 10 cm apart. Potential at centre of the line joining the two charge is:-
The capacity of an isolate conducting sphere of radius R is proportional to
Identify the wrong statement in the following.
Coulomb's law correctly describes the electric force that ______
There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
F = `(Qq)/r^2 hatr`
where the distance r is measured in cm (= 10–2 m), F in dynes (= 10–5 N) and the charges in electrostatic units (es units), where 1 es unit of charge = `1/([3]) xx 10^-9 C`
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by c = 2.99792458 × 108 m/s. An approximate value of c then is c = [3] × 108 m/s.
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Show that this gives
`1/(4pi ∈_0) = 10^-9/x^2 (N*m^2)/C^2`
With `x = 1/([3]) xx 10^-9`, we have `1/(4pi ∈_0) = [3]^2 xx 10^9 (Nm^2)/C^2`
or, `1/(4pi ∈_0) = (2.99792458)^2 xx 10^9 (Nm^2)/C^2` (exactly).
Two point charges Q each are placed at a distance d apart. A third point charge q is placed at a distance x from the mid-point on the perpendicular bisector. The value of x at which charge q will experience the maximum Coulomb's force is ______.
The ratio of the forces between two charges placed at a certain distance apart in the air and by the same distance apart in a medium of dielectric constant K is ______.
