Advertisements
Advertisements
Question
Suppose that the radius of cross-section of the wire used in the previous problem is r. Find the increase in the radius of the loop if the magnetic field is switched off. Young's modulus of the material of the wire is Y.
Solution
Given:
Radius of cross-section of the wire = r
Young's modulus of the material of the wire is Y.
As per the question, when the applied magnetic field is switched off, the tension in the wire increased and so did its length.
Young's modulus,
`Y =(stress)/"strain"`
`Y=(T//A)/(Deltal//l)`
Here,
T is the tension
A is the area of cross-section
Δl is the increse in length of the wire
`Deltal = (Tl)/(YA) = (iaBxx1)/(Yxxpir^2)`
`2pixx Deltar = (iaBxx2pia)/(Yxxpir^2)`
`Delta r =( ia^2B)/(pir^2Y)`
APPEARS IN
RELATED QUESTIONS
Write the expression for the magnetic moment `vecm`due to a planar square loop of side ‘l’ carrying a steady current I in a vector form.
In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance l as shown. Give reason to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop.

Will a current loop placed in a magnetic field always experience a zero force?
Is it possible for a current loop to stay without rotating in a uniform magnetic field? If yes, what should be the orientation of the loop?
A circular loop of area 1 cm2, carrying a current of 10 A, is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
The figure shows a circular wire loop of radius a and carrying a current i, which is placed in a perpendicular magnetic field B. (a) Consider a small part dl of the wire. Find the force on this part of the wire exerted by the magnetic field. (b) Find the force of compression in the wire.
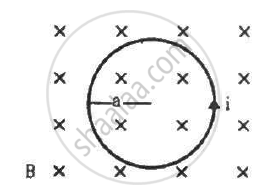
A circular loop carrying a current i is made of a wire of length L. A uniform magnetic field B exists parallel to the plane of the loop. (a) Find the torque on the loop. (b) If the same length of the wire is used to form a square loop, what would be the torque? Which is larger?
If in a moving coil galvanometer, a current I produces a deflection `theta,` then ____________.
Two galvanometers 'G1' and 'G2' require 2 mA and 3 mA respectively to produce the same deflection. Then _______.
If the net magnetic force acting on a loop is zero then ____________.
The sensitivity of moving coil galvanometer is inversely proportional to ____________.
Which one of the following statements is 'NOT' TRUE? Sensitivity of a moving coil galvanometer can be increased by ____________.
An ammeter is obtained by shunting 'n' `Omega` galvanometer with 'n' `Omega` resistance. The additional shunt required to be connected across it to double the range is ____________.
What is the magnetic moment of a current-carrying circular coil if the radius of the circular coil is 'R' and magnetic induction at the center is 'B'?
Two cylinders A and B of the same material have same length, their radii being in the ratio 1 : 2 respectively. The two are joined end to end as shown in the figure. One end of cylinder A is rigidly clamped while free end of cylinder B is twisted through an angle θ. The angle of twist of cylinder A is ______.
The initial pressure and volume of a gas enclosed in a cylinder are 2 × 105 N/m2 and 6 × 10-3 m3 respectively. If the work done in compressing the gas at constant pressure is 150 J. find the final volume of the gas.
A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is ______.


Write the formula for torque acting on rotating current carrying coil in terms of magnetic dipole moment, in vector form.
A circular coil having N turns of radius R carrying a current I is used to produce a magnetic field B at its centre O.
If this coil is opened and rewound such that the radius of the newly formed coil is 2R, carrying the same current I, what will be the magnetic field at the centre O?
