Advertisements
Advertisements
Question
The current generator Ig' shown in figure, sends a constant current i through the circuit. The wire ab has a length l and mass m and can slide on the smooth, horizontal rails connected to Ig. The entire system lies in a vertical magnetic field B. Find the velocity of the wire as a function of time.
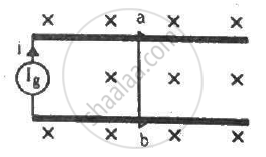
Solution
Because current i passes through the sliding wire, the magnetic force on the wire (F) is ilB.
Now,
Acceleration of the sliding wire, `a=(ilB)/m`
Velocity of the sliding wire, v = u + at
∵ u = 0
`therefore v = (ilBt)/m`
APPEARS IN
RELATED QUESTIONS
Find the condition under which the charged particles moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speed.
Two identical coils P and Q each of radius R are lying in perpendicular planes such that they have a common centre. Find the magnitude and direction of the magnetic field at the common centre of the two coils, if they carry currents equal to I and \[\sqrt{3}\] I respectively.

Sketch a schematic diagram depicting oscillating electric and magnetic fields of an em wave propagating along + z-direction ?
The motion of copper plate is damped when it is allowed to oscillate between the two poles of a magnet. What is the cause of this damping?
Two proton beams going in the same direction repel each other whereas two wires carrying currents in the same direction attract each other. Explain.
A moving charge produces
Consider a long, straight wire of cross-sectional area A carrying a current i. Let there be n free electrons per unit volume. An observer places himself on a trolley moving in the direction opposite to the current with a speed \[v = \frac{i}{\text{nAe}}\] and separation from the wire by a distance r. The magnetic field seen by the observer is very nearly
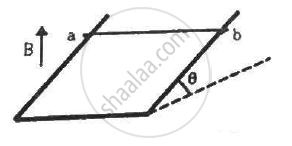
A wire ab of length l, mass m and resistance R slides on a smooth, thick pair of metallic rails joined at the bottom as shown in figure. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exists in the region. If the wire slides on the rails at a constant speed v, show that \[B = \sqrt{\frac{mg R sin\theta}{v l^2 \cos^2 \theta}}\]
Consider the situation shown in figure. The wires P1Q1 and P2Q2 are made to slide on the rails with the same speed 5 cm s−1. Suppose the 19 Ω resistor is disconnected. Find the current through P2Q2 if (a) both the wires move towards right and (b) if P1Q1 moves towards left but P2Q2 moves towards right.

A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?
A charged particle moves through a magnetic field perpendicular to its direction. Then ______.
A charged particle moving in a magnetic field experiences a resultant force ______
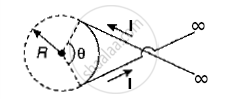
A wire carrying current i has the configuration shown in figure. For the magnetic field to be zero at the centre of the circle, θ must be:
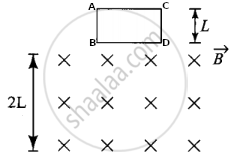
A square coil ABCD with its plane vertical is released from rest in a horizontal uniform magnetic field `vec"B"` of length 2L. The acceleration of the coil is ______.
An α particle is moving along a circle of radius R with a constant angular velocity ω. Point A lies in the same plane at a distance 2R from the centre. Point A records magnetic field produced by α particle, if the minimum time interval between two successive times at which A records zero magnetic field is 't' the angular speed ω, in terms of t is ______.
A charge Q is moving `vec"dl"` distance in the magnetic field `vec"B"`. Find the value of work done by `vec"B"`.
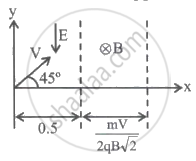
A charged particle of charge q and mass m is projected in a region that contains an electric and magnetic field as shown in the figure with velocity V at an angle of 45° with x-direction. If V = `sqrt((qE)/m)`, then net deviation in particle motion will be (neglect the effect of gravity) in a clockwise direction approx ______ °.