Advertisements
Advertisements
Question
The hypotenuse of a right-angled triangle is 26 cm and the sum of other two sides is 34 cm. Find the lengths of its sides.
Solution
Hypotenuse = 26 cm
The sum of other two sides is 34 cm.
So, let the other two sides be x cm and (34 – x) cm.
Using Pythagoras theorem,
(26)2 = x2 + (34 – x)2
676 = x2 + x2 + 1156 – 68x
2x2 – 68x + 480 = 0
x2 – 34x + 240 = 0
x2 – 10x – 24x + 240 = 0
x(x – 10) – 24(x – 10) = 0
(x – 10)(x – 24) = 0
x = 10, 24
When x = 10, (34 – x) = 24
When x = 24, (34 – x) = 10
Thus, the lengths the three sides of the right-angled triangle are 10 cm, 24 cm and 26 cm.
APPEARS IN
RELATED QUESTIONS
The hypotenuse of a right-angled triangle exceeds one side by 1 cm and the other side by 18 cm; find the lengths of the sides of the triangle.
The diagonal of a rectangle is 60 m more than its shorter side and the larger side is 30 m more than the shorter side. Find the sides of the rectangle.
The perimeter of a rectangle is 104 m and its area is 640 m2. Find its length and breadth.
A footpath of uniform width runs round the inside of a rectangular field 32 m long and 24 m wide. If the path occupies 208 m2, find the width of the footpath.
An area is paved with square tiles of a certain size and the number required is 128. If the tiles had been 2 cm smaller each way, 200 tiles would have been needed to pave the same area. Find the size of the larger tiles.
A car made a run of 390 km in ‘x’ hours. If the speed had been 4 km/hour more, it would have taken 2 hours less for the journey. Find ‘x’.
The perimeter of a rectangular field is 28 m and its area is 40 sq. m. Its sides are ______.
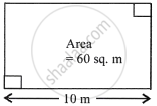
The area of the given rectangle is 60 sq. m and its longer side is 10 m, the perimeter of the rectangle is ______.
The perimeter of a square is numerically equal to its area. The perimeter of the square is ______.
The length of a rectangle is 3 m more than its width. If its area is 180 m2; the length of the rectangle is ______.
