Advertisements
Advertisements
Question
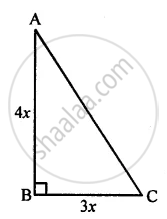
The legs of a right-angled triangle are in the ratio 4 : 3 and its area is 4056 cm2. Find the length of its legs.
Solution
Area of right-angled triangle = 4056 cm2
Legs of a right-angled triangled are in the ratio i.e. 4 : 3
Let one leg (Base) = 3x
Then second leg (altitude) = 4x
Area =`1/2xx"Base"xx"Altitude"`
= `1/2xx3"x"xx4"x"` = 6x2
∴ 6x2 = 4056
x2 = `4056/6` = 676
x = `sqrt676=sqrt(26xx26)`
∴ x = 26 cm
∴ One leg (base) = 3x = 3 × 26 = 78 cm
and second leg (altitude) 4x = 4 × 26 = 104 cm
APPEARS IN
RELATED QUESTIONS
One side of a parallelogram is 20 cm and its distance from the opposite side is 16 cm. Find the area of the parallelogram.
If the area of a rhombus is 112 cm2 and one of its diagonals is 14 cm, find its other diagonal.
Find the area of a triangle whose base is 30 cm and the height is 18 cm.
The area of a right-angled triangle is 160 cm2. If its one leg is 16 cm long, find the length of the other leg.
Find the area of an equilateral triangle whose each side is 16 cm. (Take `sqrt3`= 1.73)
Find the area of an isosceles triangle whose base is 16 cm and the length of each of the equal sides is 10 cm.
The diameter of a circle is 20 cm. Taking π = 3.14, find the circumference and its area.
A metal wire, when bent in the form of a square of largest area, encloses an area of 484 cm2. Find the length of the wire. If the same wire is bent to the largest circle, find:
(i) radius of the circle formed.
(ii) area of the circle.
The length and breadth of a rectangular paper are 35 cm and 22 cm. Find the area of the largest circle which can be cut out of this paper.
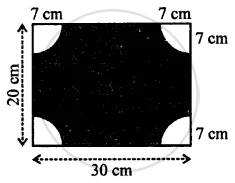
From each corner of a rectangular paper (30 cm x 20 cm) a quadrant of a circle of radius 7 cm is cut. Find the area of the remaining paper i.e., shaded portion.