Advertisements
Advertisements
Question
The monthly income of a group of 320 employees in a company is given below:
| Monthly income (thousands) | No. of employees |
| 6-7 | 20 |
| 7-8 | 45 |
| 8-9 | 65 |
| 9-10 | 95 |
| 10-11 | 60 |
| 11-12 | 30 |
| 12-13 | 5 |
Draw an ogive of the distribution on a graph paper taking 2 cm = Rs. 1000 on one axis and 2 cm = 50 employees on the other axis. From the graph detemine:
- the median wage.
- number of employee whose income is below Rs. 8,500.
- If salary of a senior employee is above Rs. 11,500, find the number of senior employee in the company.
- the upper quartile.
Solution
| Monthly income (thousands) |
No. of employees (f) |
Cumulative frequency |
| 6-7 | 20 | 20 |
| 7-8 | 45 | 65 |
| 8-9 | 65 | 130 |
| 9-10 | 95 | 225 |
| 10-11 | 60 | 285 |
| 11-12 | 30 | 315 |
| 12-13 | 5 | 320 |
| Total | 320 |
Number of employees = 320
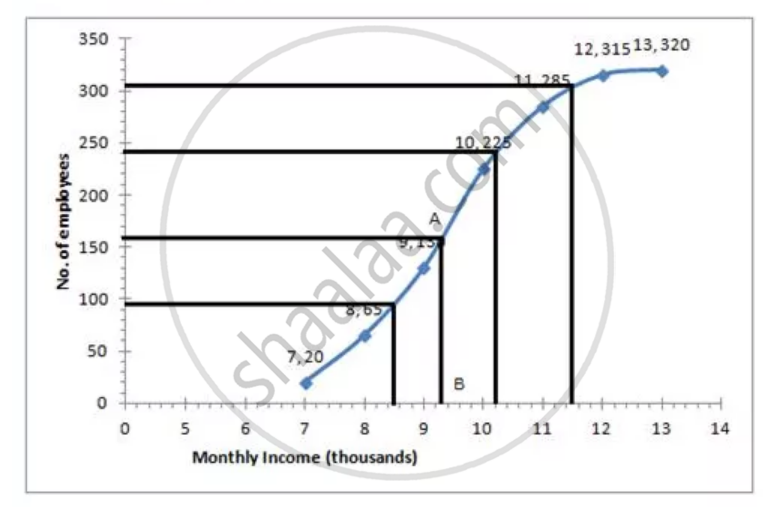
i. Median = `320/2` = 160th term
Through marks 160, draw a parallel line to x-axis which meets the curve at A. From A draw a perpendicular to x-axis meeting it at B. The value of point B is the median = Rs 9.3 thousands
ii. The number of employees with income below Rs. 8500 = 95 (approx from the graph)
iii. Number of employees with income below Rs. 11500 = 305 (approx from the graph)
Therefore number of employees with income (senior employees) = 320 - 305 = 15
iv. Upper quartile = Q3
= `320 xx 3/4`
= 240th term
= 10.3 thousands
= Rs. 10,300
APPEARS IN
RELATED QUESTIONS
The following table gives the heights of plants in centimeter. If the mean height of plants is 60.95 cm; find the value of 'f'.
| Height (cm) | 50 | 55 | 58 | 60 | 65 | 70 | 71 |
| No. of plants | 2 | 4 | 10 | f | 5 | 4 | 3 |
Find the mean (correct to one place of decimal) by using short-cut method.
|
x |
40 |
41 |
43 |
45 |
46 |
49 |
50 |
|
f |
14 |
28 |
38 |
50 |
40 |
20 |
10 |
If the mean of 11 , 14 , p , 26 , 10 , 12 , 18 , 6 is 15, find p.
Find the mean of the following frequency distribution :
| Class | 1-10 | 11-20 | 21-30 | 31-40 | 41-50 |
| Frequency | 9 | 12 | 15 | 10 | 14 |
Find the mean of: first eight natural numbers
Find the mean of: first five odd natural numbers
Find the median of 3.2, 4.8, 5.6, 5.6, 7.3, 8.9 and 9.1
The median of the data 12, 14, 23, 25, 34, 11, 42, 45, 32, 22, 44 is ___________
The median of first ten even natural numbers is ___________
Find the median of the given data: 35, 25, 34, 36, 45, 18, 28
