Advertisements
Advertisements
प्रश्न
The monthly income of a group of 320 employees in a company is given below:
| Monthly income (thousands) | No. of employees |
| 6-7 | 20 |
| 7-8 | 45 |
| 8-9 | 65 |
| 9-10 | 95 |
| 10-11 | 60 |
| 11-12 | 30 |
| 12-13 | 5 |
Draw an ogive of the distribution on a graph paper taking 2 cm = Rs. 1000 on one axis and 2 cm = 50 employees on the other axis. From the graph detemine:
- the median wage.
- number of employee whose income is below Rs. 8,500.
- If salary of a senior employee is above Rs. 11,500, find the number of senior employee in the company.
- the upper quartile.
उत्तर
| Monthly income (thousands) |
No. of employees (f) |
Cumulative frequency |
| 6-7 | 20 | 20 |
| 7-8 | 45 | 65 |
| 8-9 | 65 | 130 |
| 9-10 | 95 | 225 |
| 10-11 | 60 | 285 |
| 11-12 | 30 | 315 |
| 12-13 | 5 | 320 |
| Total | 320 |
Number of employees = 320
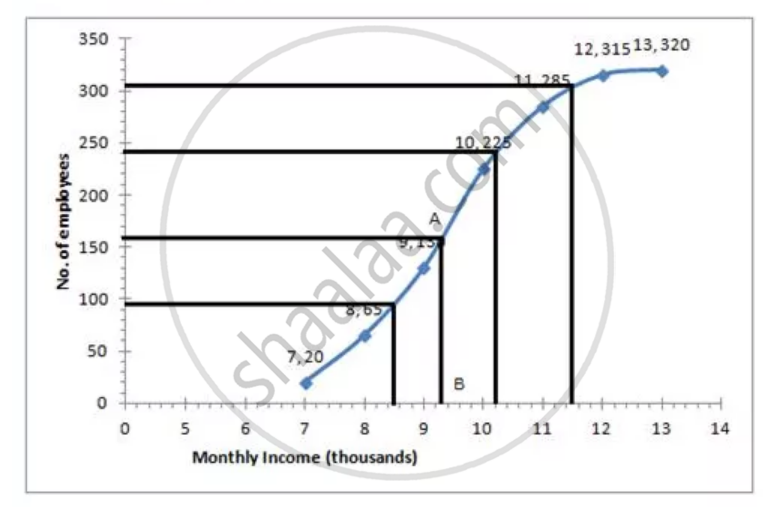
i. Median = `320/2` = 160th term
Through marks 160, draw a parallel line to x-axis which meets the curve at A. From A draw a perpendicular to x-axis meeting it at B. The value of point B is the median = Rs 9.3 thousands
ii. The number of employees with income below Rs. 8500 = 95 (approx from the graph)
iii. Number of employees with income below Rs. 11500 = 305 (approx from the graph)
Therefore number of employees with income (senior employees) = 320 - 305 = 15
iv. Upper quartile = Q3
= `320 xx 3/4`
= 240th term
= 10.3 thousands
= Rs. 10,300
APPEARS IN
संबंधित प्रश्न
If the mean of the following observations is 54, find the value of p.
| Class | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 |
| Frequency | 7 | p | 10 | 9 | 13 |
A boy scored following marks in various class tests during a term; each test being marked out of 20.
15, 17, 16, 7, 10, 12, 14, 16, 19, 12 and 16
What are his total marks?
Find the mean of the following frequency distribution by the short cut method :
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 9 | 12 | 15 | 10 | 14 |
Find the mode of the following:
6, 7, 1, 8,6,5, 9, 4, 6, 7, 1,3, 2, 6, 7,8
Find the mode of the following:
3, 4, 5, 7, 6, 3, 5, 4, 3, 5, 6, 4, 7, 5, 4, 5, 4, 3, 4, 5, 7, 6, 5, 6, 6, 7
The frequency distribution table below shows the height of 50 students of grade 10.
| Heights (in cm) | 138 | 139 | 140 | 141 | 142 |
| Frequency | 6 | 11 | 16 | 10 | 7 |
Find the median, the upper quartile and the lower quartile of the heights.
Estimate the median, the lower quartile and the upper quartile of the following frequency distribution by drawing an ogive:
| Marks | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of boys | 10 | 12 | 14 | 12 | 9 | 7 | 6 |
Find the mean of first five prime numbers.
Find the mean of: 12, 9, 6,11 and 17
Find the median of the data: 24, 36, 46, 17, 18, 25, 35
