Advertisements
Advertisements
Question
The product of the hole concentration and the conduction electron concentration turns out to be independent of the amount of any impurity doped. The concentration of conduction electrons in germanium is 6 × 1019 per cubic metref conduction electrons increases to 2 × 1023 per cubic metre. Find the concentration of the holes in the doped germanium.. When some phosphorus impurity is doped into a germanium sample, the concentration o
Solution
We know that for an intrinsic semiconductor, the concentration of electrons is equal to the concentration of holes.
The product of electron hole pair concentration always remains constant.
i.e. Number of holes × Number of conduction electrons = Constant
Initially, the number of conduction electron per cubic metre = 6 × 1019
We know,
Number of holes per cubic metre = Number of electrons per cubic metre
∴ Number of holes per cubic metre = 6 ×1019
After doping,
Number of conduction electrons per cubic metre = 2 × 1023
Now,
Let the number of holes per cubic metre be x.
As the product of electron hole pair concentration always remains constant,
\[(6 \times {10}^{19} )(6 \times {10}^{19} ) = (2 \times {10}^{23} )x\]
\[ \Rightarrow x = \frac{6 \times 6 \times {10}^{19 + 19}}{2 \times {10}^{23}} \]
\[ \Rightarrow x = 18 \times {10}^{15} = 1 . 8 \times {10}^{16}\]
APPEARS IN
RELATED QUESTIONS
Write two characteristic features to distinguish between n-type and p-type semiconductors ?
Distinguish between a conductor, a semiconductor and an insulator on the basis of energy band diagrams.
How many 1s energy states are present in one mole of sodium vapour? Are they all filled in normal conditions? How many 3s energy states are present in one mole of sodium vapour? Are they all filled in normal conditions?
The conduction band of a solid is partially filled at 0 K. Will it be a conductor, a semiconductor or an insulator?
When an electron goes from the valence band to the conduction band in silicon, its energy is increased by 1.1 eV. The average energy exchanged in a thermal collision is of the order of kT which is only 0.026 eV at room temperature. How is a thermal collision able to take some to the electrons from the valence band to the conduction band?
Let np and ne be the number of holes and conduction electrons in an intrinsic semiconductor.
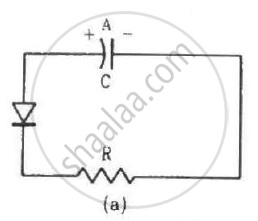
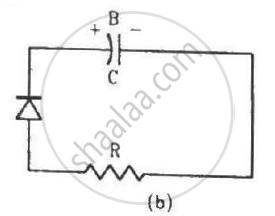
Two identical capacitors A and B are charged to the same potential V and are connected in two circuits at t = 0 as shown in figure. The charges on the capacitors at a time t = CRare, respectively,
The band gap for silicon is 1.1 eV. (a) Find the ratio of the band gap to kT for silicon at room temperature 300 K. (b) At what temperature does this ratio become one tents of the value at 300 K? (Silicon will not retain its structure at these high temperatures.)
(Use Planck constant h = 4.14 × 10-15 eV-s, Boltzmann constant k = 8·62 × 10-5 eV/K.)
When a semiconducting material is doped with an impurity, new acceptor levels are created. In a particular thermal collision, a valence electron receives an energy equal to 2kT and just reaches one of the acceptor levels. Assuming that the energy of the electron was at the top edge of the valence band and that the temperature T is equal to 300 K, find the energy of the acceptor levels above the valence band.
The band gap between the valence and the conduction bands in zinc oxide (ZnO) is 3.2 eV. Suppose an electron in the conduction band combines with a hole in the valence band and the excess energy is released in the form of electromagnetic radiation. Find the maximum wavelength that can be emitted in this process.
Find the maximum wavelength of electromagnetic radiation which can create a hole-electron pair in germanium. The band gap in germanium is 0.65 eV.
(Use Planck constant h = 4.14 × 10-15 eV-s, Boltzmann constant k = 8·62 × 10-5 eV/K.)
A semiconducting material has a band gap of 1 eV. Acceptor impurities are doped into it which create acceptor levels 1 meV above the valence band. Assume that the transition from one energy level to the other is almost forbidden if kT is less than 1/50 of the energy gap. Also if kT is more than twice the gap, the upper levels have maximum population. The temperature of the semiconductor is increased from 0 K. The concentration of the holes increases with temperature and after a certain temperature it becomes approximately constant. As the temperature is further increased, the hole concentration again starts increasing at a certain temperature. Find the order of the temperature range in which the hole concentration remains approximately constant.
(Use Planck constant h = 4.14 × 10-15 eV-s, Boltzmann constant k = 8·62 × 10-5 eV/K.)
Two radioactive substances A and B have decay constants 3λ and λ respectively. At t = 0 they have the same number of nuclei. The ratio of the number of nuclei of A to those of B will be `1/"e"` after a time interval:
If the lattice constant of this semiconductor is decreased, then which of the following is correct?
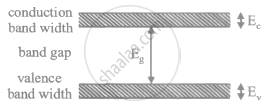
A semiconductor is cooled from T.K to T2K its resistance will
The valance of an impurity added to germanium crystal in order to convert it into p-type semiconductor is
Three photo diodes D1, D2 and D3 are made of semiconductors having band gaps of 2.5 eV, 2 eV and 3 eV, respectively. Which 0 ones will be able to detect light of wavelength 6000 Å?
With reference to semiconductor physics, answer the following question.
In which material “Forbidden band” is absent?
