Advertisements
Advertisements
Question
The two vectors \[\hat{j} + \hat{k}\] and \[3 \hat{i} - \hat{j} + 4 \hat{k}\] represents the sides \[\overrightarrow{AB}\] and \[\overrightarrow{AC}\] respectively of a triangle ABC. Find the length of the median through A.
Solution
\[\overrightarrow{AB}\] as \[\hat{j} + \hat{k}\] In ∆ABC, \[\overrightarrow{AB} = \hat{j} + \hat{k}\] and \[\overrightarrow{AC} = 3 \hat{i} - \hat{j} + 4 \hat{k}\]
Let the position vector of A be (0, 0, 0). Then, the position vectors of B and C are (0, 1, 1) and (3, −1, 4), respectively.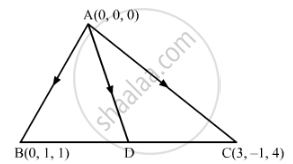
Suppose D be the mid-point of the line segment joining the points B(0, 1, 1) and C(3, −1, 4).
∴ Position vector of D \[= \frac{\left( \hat{j} + \hat{k} \right) + \left( 3 \hat{i} - \hat{j} + 4 \hat{k} \right)}{2} = \frac{3 \hat{i} + 5 \hat{k}}{2} = \frac{3}{2} \hat{i} + \frac{5}{2} \hat{k}\]
Now,
Length of the median, AD = \[\left| \overrightarrow{AD} \right| = \left| \left( \frac{3}{2} \hat{i} + \frac{5}{2} \hat{k} \right) - \left( 0 \hat{i} + 0 \hat{j} + 0 \hat{k} \right) \right| = \left| \frac{3}{2} \hat{i} + \frac{5}{2} \hat{k} \right| = \sqrt{\left( \frac{3}{2} \right)^2 + 0^2 + \left( \frac{5}{2} \right)^2} = \sqrt{\frac{34}{4}} = \sqrt{\frac{17}{2}}\] units
Notes
Disclaimer: The question has been solved by taking the vector
RELATED QUESTIONS
Find the angle between the vectors `hati-hatj and hatj-hatk`
If `veca and vecb` are perpendicular vectors, `|veca+vecb| = 13 and |veca| = 5` ,find the value of `|vecb|.`
Show that the vectors `2hati - 3hatj + 4hatk` and `-4hati + 6hatj - 8hatk` are collinear.
Evaluate the product `(3veca - 5vecb).(2veca + 7vecb)`.
Find `|vecx|`, if for a unit vector veca , `(vecx - veca).(vecx + veca) = 12`.
If `veca.veca = 0` and `veca . vecb = 0,` then what can be concluded about the vector `vecb`?
If either vector `veca = vec0` or `vecb = vec0`, then `veca.vecb = 0`. But the converse need not be true. Justify your answer with an example.
Show that the vectors `2hati - hatj + hatk, hati - 3hatj - 5hatk` and `3hati - 4hatj - 4hatk` from the vertices of a right angled triangle.
Show that the points A, B, C with position vectors `2hati- hatj + hatk`, `hati - 3hatj - 5hatk` and `3hati - 4hatj - 4hatk` respectively, are the vertices of a right-angled triangle. Hence find the area of the triangle
If \[\vec{a,} \vec{b}\] are two vectors, then write the truth value of the following statement:
\[\vec{a} = - \vec{b} \Rightarrow \left| \vec{a} \right| = \left| \vec{b} \right|\]
If \[\vec{a,} \vec{b}\] are two vectors, then write the truth value of the following statement:
\[|\vec{a}| = |\vec{b}| \Rightarrow \vec{a} = ± \vec{b} \]
If \[\vec{a,} \vec{b}\] are two vectors, then write the truth value of the following statement:
\[\left| \vec{a} \right| = \left| \vec{b} \right| \Rightarrow \vec{a} = \vec{b}\]
Define unit vector.
