Advertisements
Advertisements
Question
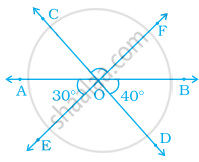
Three lines AB, CD and EF intersect each other at O. If ∠AOE = 30° and ∠DOB = 40° (Figure), find ∠COF.
Solution
∵ AB is a straight line.
∴ ∠AOE + ∠EOD + ∠DOB = 180°
⇒ ∠EOD = 180° – 30° – 40° = 110° ......(i) [∵∠AOE = 30° and ∠DOB = 40° (given)]
Now, CD and EF intersect each other at O.
∴ ∠COF = ∠EOD = 110° ......[Using (i)] [Vertically opposite angles]
Thus, ∠COF = 110°
APPEARS IN
RELATED QUESTIONS
Find the value of the angles x, y, and z in the following:

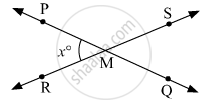
Lines PQ and RS intersect at point M. m∠PMR = x° What are the measures of ∠PMS, ∠SMQ and ∠QMR?
The angles at a point are x°, 2x°, 3x°, 4x° and 5x°. Find the value of the largest angle?
Find the angles x° and y° in the figure shown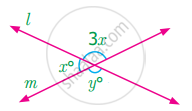
Vertically opposite angles are
In the given figure, ∠8 = 107°, what is the sum of the ∠2 and ∠4?
Statements a and b are as given below:
a: If two lines intersect, then the vertically opposite angles are equal.
b: If a transversal intersects, two other lines, then the sum of two interior angles on the same side of the transversal is 180°.
Then ______.
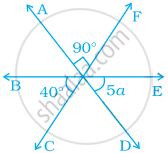
In the given figure, the value of a is ______.
Vertically opposite angles are always ______.
Vertically opposite angles are either both acute angles or both obtuse angles.
