Advertisements
Advertisements
Question
Two long straight parallel conductors carrying steady currents I1 and I2 are separated by a distance 'd'. Explain briefly, with the help of a suitable diagram, how the magnetic field due to one conductor acts on the other. Hence deduce the expression for the force acting between the two conductors. Mention the nature of this force.
Solution
Assumption: Current flows in the same direction.
Using Right hand thumb rule, the direction of the magnetic field at point P due to current I2 is perpendicular to the plane of paper and inwards.
Similarly, at point Q on X2Y2, the direction of magnetic field due to current I1 is perpendicularly outward.
Using Fleming’s left hand rule we can find the direction of forces F12 and F21 which are in opposite directions thus,
By Ampere’s circuited law, we have,

`B^2 =mu_0/(4pi) (2I_2)/d`
Now, F12 = I1LB2 (Where L ≡ length of the conductors)
`F_12 =(mu_0)/(4pi) (2I_1I_2L)/d =mu_0/(2pi)(I_1I_2L)/d`
In similar manner we get,
`F_21 =mu_0/(2pi) (I_1I_2L)/d .... (1)`
From above we get the magnitude of forces F12 and F21 are equal but in opposite direction. So,
F12 = −F21
Therefore, two parallel straight conductors carrying current in the same direction attract each other.
Similarly, we can prove if two parallel straight conductors carry currents in opposite direction, they repel each other with the same magnitude as equation (1).
RELATED QUESTIONS
Find the condition under which the charged particles moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speed.
Two identical coils P and Q each of radius R are lying in perpendicular planes such that they have a common centre. Find the magnitude and direction of the magnetic field at the common centre of the two coils, if they carry currents equal to I and \[\sqrt{3}\] I respectively.

Show with the help of a diagram how the force between the two conductors would change when the currents in them flow in the opposite directions?
Consider a long, straight wire of cross-sectional area A carrying a current i. Let there be n free electrons per unit volume. An observer places himself on a trolley moving in the direction opposite to the current with a speed \[v = \frac{i}{\text{nAe}}\] and separation from the wire by a distance r. The magnetic field seen by the observer is very nearly
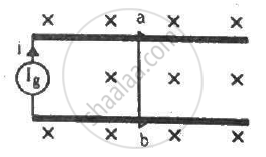
The current generator Ig' shown in figure, sends a constant current i through the circuit. The wire ab has a length l and mass m and can slide on the smooth, horizontal rails connected to Ig. The entire system lies in a vertical magnetic field B. Find the velocity of the wire as a function of time.
A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?
A charged particle moves through a magnetic field perpendicular to its direction. Then ______.
-
The presence of a large magnetic flux through a coil maintains a current in the coil if the circuit is continuous.
-
A coil of a metal wire kept stationary in a non– uniform magnetic field has an e.m.f induced in it.
-
A charged particle enters a region of uniform magnetic field at an angle of 85° to the magnetic lines of force, the path of the particle is a circle.
-
There is no change in the energy of a charged particle moving in a magnetic field although a magnetic force is acting on it.
A moving charge will gain kinetic energy due to the application of ______.
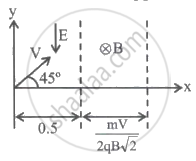
A charged particle of charge q and mass m is projected in a region that contains an electric and magnetic field as shown in the figure with velocity V at an angle of 45° with x-direction. If V = `sqrt((qE)/m)`, then net deviation in particle motion will be (neglect the effect of gravity) in a clockwise direction approx ______ °.