Advertisements
Advertisements
Question
Use the adjoining figure to find: (i) ∠BOD (ii) ∠AOC
Solution
∠AOD = 72°
∠BOC = 64°
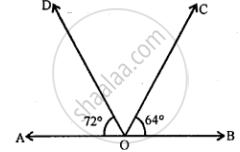
But sum of angles on the same side of a line = 180°
∴ ∠AOD + ∠COD + ∠BOC = 180°
72° + ∠COD + 64° = 180°
∠COD = 180° - (72° + 64°)
= 180° - 136° = 44°
(i) Now ∠BOD = ∠BOC + ∠COD
= 64° + 44° = 108°
(ii) ∠AOC = ∠AOD + ∠COD
= 72° + 44° = 116°
APPEARS IN
RELATED QUESTIONS
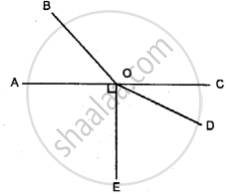
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of:
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.
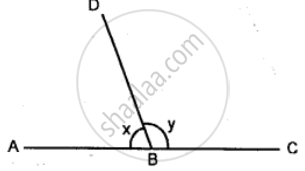
In the given diagram, ABC is a straight line. If x = 53°, find y.
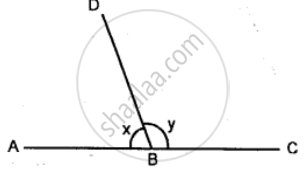
In the given diagram, ABC is a straight line. If y =`1 1/2` right angles; find x.
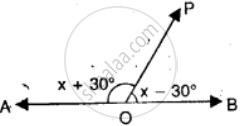
In the given figure, AOB is a straight line. Find the value of x and also answer each of the following:
(i) ∠AOP = ……..
(ii) ∠BOP = ……..
(iii) which angle is obtuse?
(iv) which angle is acute?
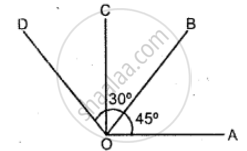
In the given figure:
(i) If ∠AOB = 45°, ∠BOC = 30° and ∠AOD= 110°; find : angles COD and BOD.
(ii) If ∠BOC = ∠DOC = 34° and ∠AOD = 120° ; find : angle AOB and angle AOC.
(iii) If ∠AOB = ∠BOC = ∠COD = 38° find : reflex angle AOC and reflex angle AOD.
Write the complement angle of: (x – 10)°
Write the supplement angle of: (x – 30)°
`3/4` of 160°
Two adjacent angles forming a linear pair are in the ratio 7:5, find the angles.
An angle is one-thirds of a straight line angle; find:
(i) the angle
(ii) the complement and the supplement of the angle obtained above.
