Advertisements
Advertisements
Question
विजय के पास कुछ केले थे और उसने उन्हें दो समूहों (ढेरियों) A एवं B में विभाजित कर लिया। उसने पहले समूह के केलों को 2 रु के 3 केले की दर से बेचा तथा दूसरे समूह के केलों को 1 रु प्रति केले की दर से बेचा और कुल 400 रु प्राप्त किए। यदि उसने पहले समूह के केलों को 1 रु प्रति केले की दर से बेचा होता तथा दूसरे समूह के केलों को 4 रु के 5 केले की दर से बेचा होता, तो उसे कुल 460 रु प्राप्त होते। ज्ञात कीजिए कि उसके पास कुल कितने केले थे।
Solution
माना कि लॉट A और B में केलों की संख्या क्रमशः x और y है।
स्थिति I: 3 केले के लिए ₹ 2 की दर से पहले लॉट की लागत + ₹ 1 प्रति केले की दर से दूसरे लॉट की लागत = ₹ 400
⇒ `2/3x + y` = 400
⇒ 2x + 3y = 1200 ......(i)
स्थिति II: पहले लॉट की लागत ₹ 1 प्रति केले की दर से + दूसरे लॉट की लागत 5 केले के लिए ₹ 4 की दर से = प्राप्त राशि
⇒ `x + 4/5y` = 460
⇒ 5x + 4y = 2300 ......(ii)
समीकरण (i) को 4 से और समीकरण (ii) को 3 से गुणा करने और फिर उन्हें घटाने पर, हमें प्राप्त होता है।
(8x + 12y) – (15x + 12y) = 4800 – 6900
⇒ – 7x = – 2100
⇒ x = 300
अब, x का मान समीकरण (i) में रखने पर, हमें प्राप्त होता है।
2 × 300 + 3y = 1200
⇒ 600 + 3y = 1200
⇒ 3y = 1200 – 600
⇒ 3y = 600
⇒ y = 200
∴ केलों की कुल संख्या = समूह A में केलों की संख्या + समूह B में केलों की संख्या
= x + y
= 300 + 200
= 500
अत:, उसके पास 500 केले थे।
APPEARS IN
RELATED QUESTIONS
निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं। अद्वितीय हल की स्थिति में, उसे व्रज-गुणन विधि से ज्ञात कीजिए।
3x - 5y = 20
6x - 10y = 40
निम्नलिखित आयत में x और y के मान ज्ञात कीजिए:
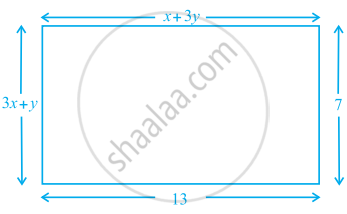
निम्नलिखित समीकरण-युग्म को हल कीजिए:
`4x + 6/y = 15, 6x - 8/y = 14, y ≠ 0`
निम्नलिखित समीकरण-युग्म को हल कीजिए:
`1/(2x) - 1/y = -1, 1/x + 1/(2y) = 8, x, y ≠ 0`
निम्नलिखित समीकरण-युग्म को हल कीजिए:
43x + 67y = – 24, 67x + 43y = 24
अंकिता अपने घर तक 14 km की दूरी आंशिक रूप से रिक्शा से और आंशिक रूप से बस द्वारा तय करती है। यदि वह 2 km दूरी रिक्शा से तथा शेष दूरी बस से तय करे, तो उसे कुल दूरी चलने में आधा घंटा लगता है। दूसरी ओर, यदि वह 4 km दूरी रिक्शा से और शेष दूरी बस से चले, तो उसे 9 मिनट अधिक लगते हैं। रिक्शा की चाल और बस की चाल ज्ञात कीजिए।
एक मोटरबोट धारा के प्रतिकूल 30 km और धारा के अनुकूल 28 km जाने में 7 घंटे का समय लगाती है। वह धारा के प्रतिकूल 21 km जाकर 5 घंटे में वापस आ सकती है। शांत जल में नाव की चाल और धारा की चाल ज्ञात कीजिए।
दो अंकों की एक संख्या या तो अंकों के योग को 8 से गुणा कर और फिर उसमें से 5 घटा कर प्राप्त होती है या अंकों के अंतर को 16 से गुणा करके और फिर उसमें 3 जोड़ने पर प्राप्त होती है। वह संख्या ज्ञात कीजिए।
रेल के एक आधे टिकट के लिए, पूरे किराए का आधा तथा आरक्षण शुल्क उतना ही देना पड़ता है जितना पूरे टिकट के लिए देना होता है। स्टेशन A से स्टेशन B तक के लिए एक प्रथम श्रेणी के आरक्षित टिकट की लागत 2530 रु है। साथ ही, A से B तक के लिए, एक प्रथम श्रेणी टिकट और एक प्रथम श्रेणी आधे टिकट की लागत 3810 रु है। स्टेशन A से स्टेशन B तक का प्रथम श्रेणी का पूरा किराया ज्ञात कीजिए तथा साथ ही एक टिकट पर आरक्षण शुल्क भी ज्ञात कीजिए।
एक दुकानदार ने एक साड़ी 8% लाभ पर और एक स्वेटर 10% बट्टे पर बेचा, जिससे उसे 1008 रु की धनराशि प्राप्त हुई। यदि उसने साड़ी 10% लाभ और स्वेटर को 8% बट्टे पर बेचा होता, तो उसे 1028 रु की धनराशि प्राप्त होती। साड़ी का क्रय मूल्य और स्वेटर का सूची मूल्य (बट्टे से पहले का मूल्य) ज्ञात कीजिए।
