Advertisements
Advertisements
Question
वक्र y = 2`sqrtx` के अंतर्गत x = 0 और x = 1 रेखाओं के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution
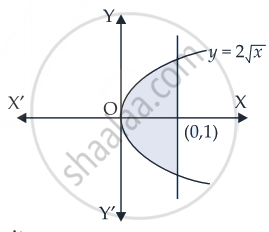
वक्रों को देखते हुए y = `2sqrt(x)`, x = 0 और x = 1.
y = `2sqrt(x)`
⇒ y2 = 4x ......(परवलय)
वाँछित क्षेत्रफल = `int_0^1 (2sqrt(x)) "d"x`
= `2 xx 2/3 [x^(3/2)]_0^1`
= `4/3 [(1)^(3/2) - 0]`
= `4/3` वर्ग इकाई
इस प्रकार, वाँछित क्षेत्रफल = `4/3` वर्ग इकाई
APPEARS IN
RELATED QUESTIONS
समाकलन विधि का उपयोग करते हुए, रेखाओं 2x + y = 4, 3x – 2y = 6 एवं x – 3y + 5 = 0 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
परवलय y2 = 2x और सरल रेखा x - y = 4 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

वक्र x = 3 cost, y = 2 sint से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
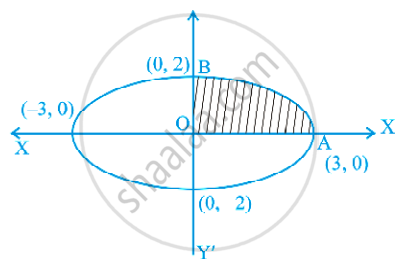
x-अक्ष के ऊपर परवलय y2 = ax और वृत्त x2 + y2 = 2ax के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
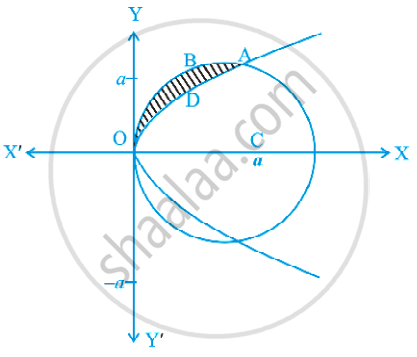
वृत्त x2 + y2 = 2 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल बराबर है
वक्र y = x2 और रेखा y = 16 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र y2 = 9x, और y = 3x से परिबद्ध क्षेत्रफल का क्षेत्रफल ज्ञात कीजिए।
वक्र y = x3 , y = x + 6 और x = 0 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y2 = 4x और x2 = 4y से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
y2 = 9x और y = x बीच में पड़ने वाले क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
रेखा x = 2 और परवलय y2 = 8x से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
समाकलन का इस्तेमाल करते हुए, रेखा 2y = 5x + 7, x-अक्ष तथा x = 2 और x = 8 रेखाओं से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = `sqrt(x - 1)` का अंतराल [1, 5] में एक संभावित आकृति खींचिए। इस वक्र के अंतर्गत तथा x = 1 और x = 5 रेखाओं के बीच के क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = –x2 और सरल रेखा x + y + 2 = 0 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
प्रथम चतुर्थाश में वक्र y = `sqrtx, x = 2y + 3` और x-अक्ष से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
वक्र y2 = 2x और x2 + y2 = 4x से परिंबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
x = 0 और x = 2π के बीच वक्र y = sinx द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
क्षेत्र `{(x, "y") : "y"^2 ≤ 6"a"x "और" x^2 + "y"^2≤ 16"a"^2}` का एक संभावित आकृति खींचिए। साथ ही,समाकलन की विधि द्वारा इस क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
रेखा x + 2y = 2, y – x = 1 और 2x + y = 7 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
रेखाओं y = 4x + 5, y = 5 – x और 4y = x + 5 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
y-अक्ष, y = cosx, y = sinx, 0 ≤ x ≤ `pi/2` से परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र y = `sqrt(16 - x^2)` और x-अक्ष से परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र y = sinx द्वारा कोटि x = 0, और x = `pi/2` तथा x-अक्ष के बीच परिबद्ध क्षेत्र का क्षेत्रफल है
वृत्त x2 + y2 = 1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
वक्र x = 2y + 3 तथा y = 1 और y = –1 रेखाओं द्वारा परिबद्ध क्षेत्र का क्षेत्रफल है
