Advertisements
Advertisements
Question
यदि sinθ = `7/25`, तो cosθ तथा tanθ का मान ज्ञात कीजिए।
Solution 1
sin2θ + cos2θ = 1
∴ `(7/25)^2 + cos^2theta = 1` ...............`(∵ sinθ = 7/25)`
∴ `49/625 + cos^2θ = 1`
∴ cos2θ = 1 - `49/625`
∴ cos2θ = `(625 - 49)/625`
∴ cos2θ = `576/625`
∴ cosθ = `24/25` .........(दोनों पक्षों का वर्गमूल लेने पर)
tanθ = `sintheta/costheta`
∴ tanθ = `((7/25))/((24/25))`
∴ tanθ = `7/25 xx 25/24`
∴ tanθ = `7/24`
cosθ = `underline(24/25)`, tanθ = `underline(7/24)`.
Solution 2
sinθ = `7/25` .....................(दिया है |) .............(1)
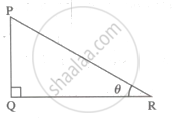
मानो कि, ΔPQR में, ∠PQR = 90 और ∠PRQ = θ
sinθ = `"PQ"/"PR"` ....................(2)
∴ `"PQ"/"PR" = 7/25` ...........[(1) और (2) से]
∴ PQ = 7k और PR = 25k
ΔPQR में,
∠PQR = 90°
∴ पायथागोरस के प्रमेय से,
`"PR"^2 = "PQ"^2 + "QR"^2`
∴ `(25k)^2 = (7k)^2 + ("QR")^2`
∴ `625k^2 = 49k^2 + "QR"^2`
∴ `"QR"^2 = 625k^2 - 49k^2`
∴ `"QR"^2 = 576k^2`
∴ QR = 24k .................(दोनों पक्षों का वर्गमूल लेने पर)
cosθ = `"QR"/"PR" = (24k)/(25k) = 24/15`
tanθ = `"PQ"/"QR" = (7k)/(24k) = 7/24`
cosθ = `underline(24/25)` और tanθ = `underline(7/24)`.
APPEARS IN
RELATED QUESTIONS
यदि cotθ = `40/9` तो cosecθ तथा sinθ का मान ज्ञात कीजिए।
सिद्ध कीजिए।
(secθ - cosθ)(cotθ + tanθ) = tanθ secθ
सिद्ध कीजिए।
`1/(sectheta - tantheta) = sectheta + tantheta`
सिद्ध कीजिए।
`tanA/(1 + tan^2A)^2 + cotA/(1 + cot^2A)^2 = sinA cosA`
सिद्ध कीजिए।
sec2θ + cosec2θ = sec2θ × cosec2θ
सिद्ध कीजिए।
tan4θ + tan2θ = sec4θ - sec2θ
सिद्ध कीजिए।
`tantheta/(sectheta + 1) = (sectheta - 1)/tantheta`
सिद्ध कीजिए।
`(sintheta - costheta + 1)/(sintheta + costheta - 1) = 1/(sectheta - tantheta)`
नीचे दिए गए बहुवैकल्पिक प्रश्न के उत्तर का सही विकल्प चुनकर लिखिए।
1 + tan2θ = कितना?
सिद्ध कीजिए: cotθ + tanθ = cosecθ × secθ
हल:
बायाँ पक्ष = cotθ + tanθ
= `cosθ/sinθ + sinθ/cosθ`
= `(square + square)/(sinθ xx cosθ)`
= `1/(sinθ xx cosθ)` ............... `square`
= `1/sinθ xx 1/square`
= cosecθ × secθ
∴ बायाँ पक्ष = दायाँ पक्ष
∴ cotθ + tanθ = cosecθ × secθ
