Advertisements
Advertisements
Question
यह दिया है कि ∠ XYZ = 64° है और XY को बिंदु P तक बढाया गया है। दी हुई सुचना से एक आकृति खींचिए। यदि किरण YQ, ∠ZYP को समद्विभाजित करती है, तो ∠XYQ और प्रतिवर्ती ∠QYP के मान ज्ञात कीजिए।
Solution
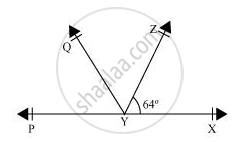
यह दिया गया है कि रेखा YQ, ∠PYZ को समद्विभाजित करती है।
इसलिये, ∠QYP = ∠ZYQ
यह देखा जा सकता है कि PX एक रेखा है। किरणें YQ और YZ इस पर खड़ी होती हैं।
∴ ∠XYZ + ∠ZYQ + ∠QYP = 180°
⇒ 64° + ∠ZYQ + ∠QYP = 180° ...[∵ ∠XYZ = 64° (दिया है)]
⇒ 64° + 2∠QYP = 180° ...[YQ, ∠ZYP को समद्विभाजित करता है, इसलिए ∠QYP = ∠ZYQ]
⇒ 2∠QYP = 180° − 64°
⇒ 2∠QYP = 116°
⇒ ∠QYP = `(116°)/2`
⇒ ∠QYP = 58°
साथ ही, ∠ZYQ = ∠QYP = 58°
प्रतिवर्ती ∠QYP = 360° − 58°
प्रतिवर्ती ∠QYP = 302°
चूँकि, ∠XYQ = ∠XYZ + ∠ZYQ
⇒ ∠XYQ = 64° + ∠QYP ...[∵ ∠XYZ = 64° (दिया है) और ∠ZYQ = ∠QYP]
⇒ ∠XYQ = 64° + 58° ...[∠QYP = 58°]
⇒ ∠XYQ = 122°
इस प्रकार, ∠XYQ = 122° और प्रतिवर्ती ∠QYP = 302°
APPEARS IN
RELATED QUESTIONS
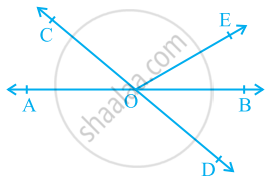
दी गई आकृति में, रेखाएँ AB और CD, बिंदु O पर प्रतिच्छेद करती हैं। यदि ∠AOC + ∠BOE = 70° है और ∠BOD = 40° है, तो ∠BOE और प्रतिवर्ती ∠COE ज्ञात कीजिए।
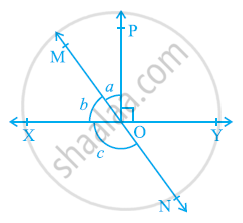
आकृति में रेखाएँ XY और MN बिंदु O पर प्रतिच्छेद करती हैं। यदि ∠POY = 90° और a : b = 2 : 3 है तो c ज्ञात कीजिए।
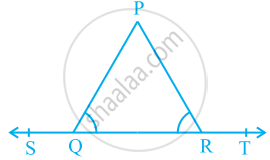
आकृति में, यदि ∠PQR = ∠PRQ है, सिद्ध कीजिए कि ∠PQS = ∠PRT है।
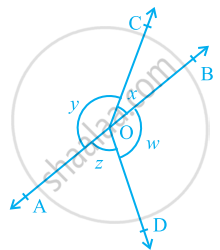
आकृति में, यदि x + y = w + z है, तो सिद्ध कीजिए कि AOB एक रेखा है।
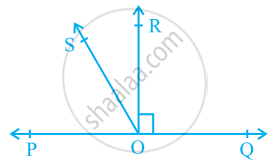
आकृति में, POQ एक रेखा है। किरण OR रेखा PQ पर लम्ब है। किरणों OP और OR के बीच में OS एक अन्य किरण है। सिद्ध कीजिए:
∠ROS = `1/2` (∠QOS − ∠POS)
क्या किसी त्रिभुज के दो अधिक कोण हो सकते हैं? अपने उत्तर के लिए कारण दीजिए।
कोणों 53°, 64° और 63° वाले कितने त्रिभुज खींचे जा सकते हैं? अपने उत्तर के लिए कारण दीजिए।
