Advertisements
Advertisements
Question
क्या किसी त्रिभुज के दो अधिक कोण हो सकते हैं? अपने उत्तर के लिए कारण दीजिए।
Solution
हम जानते हैं कि, त्रिभुज के तीनों कोणों का योग 180° के बराबर होता है।
साथ ही, अधिक कोण वह होता है जिसका मान 90° से अधिक लेकिन 180° से कम होता है।
यदि त्रिभुज में दो अधिक कोण हैं, तो कम से कम दो कोण ऐसे होते हैं जो प्रत्येक 91° के होते हैं।
इन दोनों कोणों को जोड़ने पर,
दोनों कोणों का योग = 91° + 91°
⇒ दोनों कोणों का योग = 182°
यह पहले से ही तीसरे कोण पर विचार किए बिना त्रिभुज के तीन कोणों के योग से अधिक है।
पुनः, यदि हम उस स्थिति पर विचार करें जहाँ त्रिभुज का एक कोण 90° है, तो हमें एक समकोण त्रिभुज प्राप्त होता है। त्रिभुज के उस गुण को पूरा करने के लिए शेष दो कोण 90° से कम होने चाहिए, जो बताता है कि त्रिभुज के तीनों कोणों का योग 180° के बराबर होना चाहिए।
इस प्रकार, एक त्रिभुज के दो अधिक कोण नहीं हो सकते।
APPEARS IN
RELATED QUESTIONS
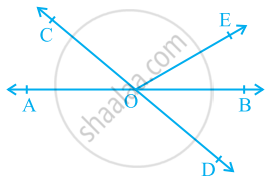
दी गई आकृति में, रेखाएँ AB और CD, बिंदु O पर प्रतिच्छेद करती हैं। यदि ∠AOC + ∠BOE = 70° है और ∠BOD = 40° है, तो ∠BOE और प्रतिवर्ती ∠COE ज्ञात कीजिए।
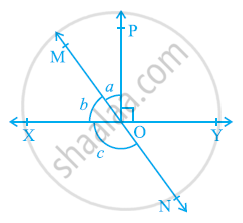
आकृति में रेखाएँ XY और MN बिंदु O पर प्रतिच्छेद करती हैं। यदि ∠POY = 90° और a : b = 2 : 3 है तो c ज्ञात कीजिए।
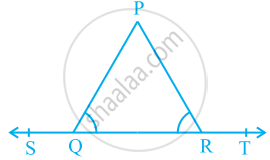
आकृति में, यदि ∠PQR = ∠PRQ है, सिद्ध कीजिए कि ∠PQS = ∠PRT है।
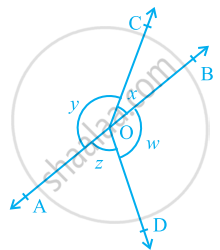
आकृति में, यदि x + y = w + z है, तो सिद्ध कीजिए कि AOB एक रेखा है।
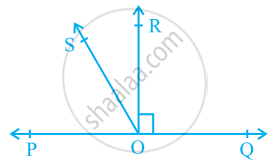
आकृति में, POQ एक रेखा है। किरण OR रेखा PQ पर लम्ब है। किरणों OP और OR के बीच में OS एक अन्य किरण है। सिद्ध कीजिए:
∠ROS = `1/2` (∠QOS − ∠POS)
यह दिया है कि ∠ XYZ = 64° है और XY को बिंदु P तक बढाया गया है। दी हुई सुचना से एक आकृति खींचिए। यदि किरण YQ, ∠ZYP को समद्विभाजित करती है, तो ∠XYQ और प्रतिवर्ती ∠QYP के मान ज्ञात कीजिए।
कोणों 53°, 64° और 63° वाले कितने त्रिभुज खींचे जा सकते हैं? अपने उत्तर के लिए कारण दीजिए।
