Topics
Geometrical Constructions
- Concept of Angle Bisector
- Drawing a Perpendicular to a Line
- The Property of the Angle Bisectors of a Triangle
- Perpendicular Bisectors of the Sides of an Acute-angled Triangle
- Perpendicular Bisectors of the Sides of an Obtuse-angled Triangle
- Construction of Triangles
- Constructing a Triangle When the Length of Its Three Sides Are Known (SSS Criterion)
- Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle Between Them Are Known. (SAS Criterion)
- Construct a Triangle Given Two Angles and the Included Side
- Construct a Right-angled Triangle Given the Hypotenuse and One Side
- Congruence Among Line Segments
- Congruence of Angles
- Congruence of Circles
Multiplication and Division of Integers
HCF and LCM
Angles and Pairs of Angles
Operations on Rational Numbers
Indices
- Concept of Exponents
- Concept of Square Number
- Concept of Cube Number
- Laws of Exponents
- Multiplying Powers with the Same Base
- Dividing Powers with the Same Base
- Taking Power of a Power
- Multiplying Powers with Different Base and Same Exponents
- Dividing Powers with Different Base and Same Exponents
- Numbers with Exponent Zero, One, Negative Exponents
- Miscellaneous Examples Using the Laws of Exponents
- Crores
- Finding the Square Root of a Perfect Square
Joint Bar Graph
- Concept of Joint Bar Graph
- Interpretation of a Joint Bar Graph
- Drawing a Joint Bar Graph
Algebraic Expressions and Operations on Them
- Terms, Factors and Coefficients of Expression
- Classification of Terms in Algebra
- Algebraic Expressions
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Multiplication of Algebraic Expressions
- Multiplying Monomial by Monomials
- Multiplying a Monomial by a Binomial
- Multiplying a Binomial by a Binomial
- Equations in One Variable
Direct Proportion and Inverse Proportion
Banks and Simple Interest
Circle
- Basic Concept of Circle
- Circumference of a Circle
- Relationship Between Circumference and Diameter
- Arc of the Circle
- Central Angle and the Measure of an Arc
Perimeter and Area
Pythagoras’ Theorem
Algebraic Formulae - Expansion of Squares
Statistics
Notes
Construct a Right-angled Triangle Given the Hypotenuse and One Side:
1) Draw ∆LMN such that m∠LMN = 90°, hypotenuse = 5 cm, l(MN) = 3 cm.
Let us draw the rough figure using the given information.
As m∠LMN = 90°, we draw a right-angled triangle approximately and mark the right angle. Thus we show the given information in the rough figure.
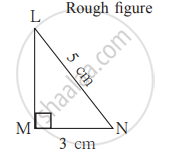
Steps:
- As shown in the rough figure, draw the base seg MN of length 3 cm.
- At point M of seg MN, draw ray MT to make an angle of 90° to seg MN.
- Opening the compass to 5 cm and with the point at N, draw an arc to cut seg MT at L.
∆LMN is the required triangle.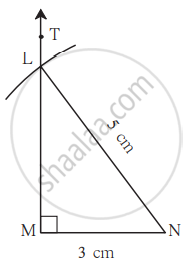
- Note that a similar figure can be drawn on the other side of the base.
Shaalaa.com | Drawing a Right Angled Triangle
to track your progress
Series: Construct a Right-angled Triangle Given the Hypotenuse and One Side
0%
