Topics
Geometrical Constructions
- Concept of Angle Bisector
- Drawing a Perpendicular to a Line at a Point on the Line
- The Property of the Angle Bisectors of a Triangle
- Perpendicular Bisectors of the Sides of an Acute-angled Triangle
- Perpendicular Bisectors of the Sides of an Obtuse-angled Triangle
- Construction of Triangles
- Constructing a Triangle When the Length of Its Three Sides Are Known (SSS Criterion)
- Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle Between Them Are Known. (SAS Criterion)
- Construct a Triangle Given Two Angles and the Included Side
- Construct a Right-angled Triangle Given the Hypotenuse and One Side
- Congruence Among Line Segments
- Congruence of Angles
- Congruence of Circles
Multiplication and Division of Integers
- Concept for Natural Numbers
- Concept for Whole Numbers
- Negative and Positive Numbers
- Concept of Integers
- Concept for Ordering of Integers
- Addition of Integers
- Subtraction of Integers
- Multiplication of a Positive and a Negative Integers
- Multiplication of Two Negative Integers
- Multiplication of Two Positive Integers
- Division of Integers
HCF and LCM
Angles and Pairs of Angles
Operations on Rational Numbers
- Rational Numbers
- Addition of Rational Number
- Additive Inverse of Rational Number
- Subtraction of Rational Number
- Multiplication of Rational Numbers
- Division of Rational Numbers
- Rational Numbers Between Two Rational Numbers
- Decimal Representation of Rational Numbers
- BODMAS - Rules for Simplifying an Expression
Indices
- Concept of Exponents
- Concept of Square Number
- Concept of Cube Number
- Laws of Exponents
- Multiplying Powers with the Same Base
- Dividing Powers with the Same Base
- Taking Power of a Power
- Multiplying Powers with Different Base and Same Exponents
- Dividing Powers with Different Base and Same Exponents
- Numbers with Exponent Zero, One, Negative Exponents
- Miscellaneous Examples Using the Laws of Exponents
- Crores
- Finding the Square Root of a Perfect Square
Joint Bar Graph
- Concept of Joint Bar Graph
- Interpretation of a Joint Bar Graph
- Drawing a Joint Bar Graph
Algebraic Expressions and Operations on Them
- Algebraic Expressions
- Terms, Factors and Coefficients of Expression
- Like and Unlike Terms
- Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Multiplication of Algebraic Expressions
- Multiplying Monomial by Monomials
- Multiplying a Monomial by a Binomial
- Multiplying a Binomial by a Binomial
- Equations in One Variable
Direct Proportion and Inverse Proportion
Banks and Simple Interest
Circle
- Concept of Circle
- Circumference of a Circle
- Relationship Between Circumference and Diameter
- Arc of the Circle
- Central Angle and the Measure of an Arc
Perimeter and Area
Pythagoras’ Theorem
Algebraic Formulae - Expansion of Squares
Statistics
Definition
Central Angle: An angle whose vertex is the centre of the circle is called a central angle.
Notes
Central Angle and the Measure of an Arc:
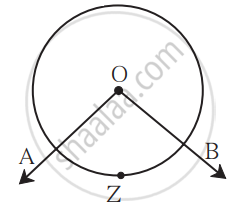
An angle whose vertex is the centre of the circle is called a central angle.
In the figure, ‘O’ is the vertex of the ∠AOB.
The ∠AOB in the figure is the central angle corresponding to arc AZB. The measure of the angle subtended at the centre by an arc is taken to be the measure of the arc.
1. The measure of a minor arc:
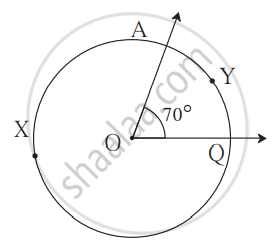
In the above figure, the measure of ∠AOQ = 70°.
∴ Measure of the minor arc AYQ is 70°.
It is written as m(arc AYQ) = 70°.
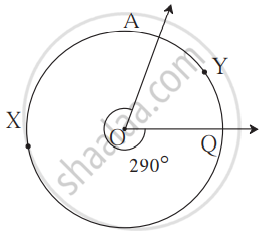
2. The measure of a major arc:
Measure of a major arc = 360° - measure of the corresponding minor arc
∴ Measure of major arc AXQ in the figure = 360° - 70° = 290°
3. The measure of a circle:
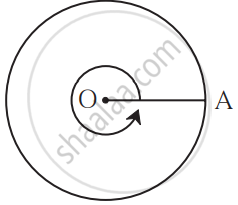
When the radius OA of a circle turns anti-clockwise, as shown in the above figure, through a complete angle, it turns through an angle that measures 360°. Its endpoint A completes one circle. The angle subtended at the center by the circle is 360°.
∴ The measure of the complete circle is 360°.
4. Measure of a semicircular arc:

The measure of a semicircular arc = 180°.
Shaalaa.com | Central Angles, Circle Arcs, Angle Measurement, Major Arcs vs Minor Arcs
Series: Central Angle and the Measure of an Arc
Related QuestionsVIEW ALL [5]
Find the central angle of the shaded sectors (each circle is divided into equal sectors).
| Sectors | 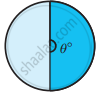 |
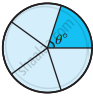 |
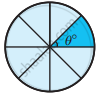 |
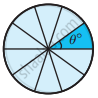 |
| Central angle of each sector (θ°) |