Topics
Number Systems
Program Analysis
Introduction to C+ +
- Introduction to C++
- Character Sets
- Standard I/O Strems in C++
- Type Modifiers
- C++ Data Types
- Variables in C++
- Constants
- Compiler Tokens
- Operators in C++
- Comments in C++
- Scope and Visibility
- Control Statements
- Functions in C++
- Default Arguments
- Techniques used to pass Variables into C++ Functions
- Function Overloading
- Inline Functions
- Recursion
- Pointers in C++
- Arrays in C++
- References
- Type Conversion in Expressions
Visual Basic
- Introduction to Visual Basic
- One language Three Editions
- Study Of Integrated Development Environment (IDE)
- Visual Basic Programming
- Few Common Methods
Introduction to Networking and Internet
- Introduction to Networking and Internet
- Networking Terms and Concepts
- Types of Networks
- Network Security
- Network Configurations
- Network Applications
- Introduction to binary number system
- Advantages of binary code and its Positive and negative logic system
- Radix and Binary Counting
Introduction to binary number system
There are only two digits in the binary system, namely, 0 and 1. Binary number system, where bi-means two, and two symbols are used as '0' and '1'. It use basic ten symbols or numbers from 0 to 9 but in digital circuits The base or radix of a binary number system is two. A binary digit '0' or '1' is called a bit. Four bits form a nibble, and eight bits form a byte. We deal in larger units called kilobyte, megabyte, and gigabyte.
Advantages of binary code and its Positive and negative Logic System
1. Binary coding simplifies the design of digital circuits like computers, calculators, and other digital systems
2. Binary can represent large amounts of data compactly using bits and bytes (e.g., ASCII for characters)
3. Different logic can be applied behind the two numbers, such as if we take a lamp, meter, or electric signal to represent these numbers, then:
For Example,
| Logic | 0 | 1 |
| Lamp | OFF | ON |
| Voltmeter | 0V | +5V and so on |
4. It is very easy to perform mathematical and Logical operations and Conversion of binary to decimal and decimal to binary
5. The Binary Number system is more accurate, fast, and readable number system It can be executed quickly by digital systems, leading to better performance.
Positive and negative logic system:
In positive logic, the higher voltage level indicates level 1, and in negative logic it indicates level 0. e.g., if levels are +5V and 0V, then in positive logic +5V indicates level 1 and in negative logic 0V indicates level 1. In the case of a lamp in positive logic, the level 1 logic is lamp ON, and in negative logic, the level 1 logic is lamp OFF.
Radix and Binary Counting
Radix is a number, which indicates the base of a specific number system. This number represents the total symbols of the system and the weightage or power of each digit. For example:
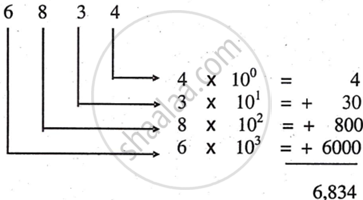
1) The radix for the decimal number system is '10' because total symbols are 10 from 0 to 9. Similarly, the weightage of each digit is in power of 10. Suppose number is six thousand eight hundred and thirty-four, then it is represented as (6 8 3 4)10 The subscript '10' indicates that the number is a decimal number. Its value is calculated as follows:
100 = 1
101 = 10
102 = 100
103 = 1000
2) In this way, if we take a binary number system, then its radix is '2' because symbols are only two (0 and 1). A number in binary number system is represented as (101011)2 Multiplying each 0 and 1 by a power of 2 and adding them can calculate its value.
| Number System | Radix | Symbols |
| 1) Decimal Number System | 10 | 0,1,... 8,9 |
| 2) Binary Number System | 2 | 0 and 1 |
| 3) Octal Number System | 8 | 0,1,......7 |
| 4) Hexadecimal Number System | 16 | 0,l,... 8,9,A,B, ... F |
Decimal counting:
The decimal counting is in a sequence like 0, 1, 2, 3, ---- 9, 10, 11, ---- 99, 100, etc. To get binary counting, take the decimal numbers in sequence and take those numbers in sequence, which contain only 0 and 1
0 , 1 ,`\cancel(2)`---10 , 11,---100 , 101 ,`\cancel(102)`---110 ,`\cancel(777)`,---1000 , 1001 , `\cancel(1003) `---
| Binary Number | Decimal Value | Binary Number | Decimal Value |
| 0 | 0 | 110 | 6 |
| 1 | 1 | 111 | 7 |
| 10 | 2 | 1000 | 8 |
| 11 | 3 | 1001 | 9 |
| 100 | 4 | 1010 | 10 |
| 101 | 5 | 1011 | 11 |
