Topics
Number Systems
Program Analysis
Introduction to C+ +
- Introduction to C++
- Character Sets
- Standard I/O Strems in C++
- Type Modifiers
- C++ Data Types
- Variables in C++
- Constants
- Compiler Tokens
- Operators in C++
- Comments in C++
- Scope and Visibility
- Control Statements
- Functions in C++
- Default Arguments
- Techniques used to pass Variables into C++ Functions
- Function Overloading
- Inline Functions
- Recursion
- Pointers in C++
- Arrays in C++
- References
- Type Conversion in Expressions
Visual Basic
- Introduction to Visual Basic
- One language Three Editions
- Study Of Integrated Development Environment (IDE)
- Visual Basic Programming
- Few Common Methods
Introduction to Networking and Internet
- Introduction to Networking and Internet
- Networking Terms and Concepts
- Types of Networks
- Network Security
- Network Configurations
- Network Applications
- Introduction to Hexadecimal Number System
- Hex to decimal conversion
- Decimal to Hexadecimal conversion
- Hex to Binary and Binary to Hex conversion
Introduction to Hexadecimal Number System
The hexadecimal number system It consists of 16 unique symbols (0–9, A–F) and is called the base 16 system. Each alphanumeric digit is represented as a group of 4 binary digits because 4 bits (24 = 16) are sufficient to represent 16 alphanumeric symbols Hexadecimal numbers are widely used in microprocessor work and can be easily converted to binary, with each hex digit represented by a four-bit binary number.
Hex to decimal conversion
The decimal equivalent of a hexadecimal number equals the sum of all hexadecimal digits multiplied by their weights. In the hexadecimal number system, the weight of each position of digit is in powers of 16
1) (2 C 6 E)16
2 C 6 E
= (2 x 163) + (C x 162) + (6 x 161) + (E x 160)
= (2 x 4096) + (12 x 256) + (6 x 16) + (14 x 1)
= 8192 + 3072 + 96 + 14
2) (3A.2F)16 = 3 x 161 + 10 x 160 + 2 x 16-1 + 15 x 16-2
= `48 + 10 + 2/16 + 15/16^2`
= (58.1836)10
Decimal to Hexadecimal conversion
For conversion from decimal to hexadecimal, we can keep by dividing the decimal number by 16 (for the integer part) and multiplying by 16 for the fractional part. For the integer part, remainders are arranged in reverse order, and for the fractional part, carries are arranged in forward order.
1) Integer part
(928)10
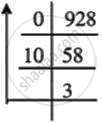
(928)10 = (3A0)16
2) Fractional part
0.5
×16
8.0
↓
8 (0.5)10 = (0.8)16
Therefore, (95.5)10 = (5F.8)16
Hex to Binary and Binary to Hex conversion
Hexadecimal to Binary Conversion:
To convert a hexadecimal number into a binary number, convert each hex digit into a 4-bit binary code, just like 8421 BCD
1) Convert (5AD)16 in to binary
= 5 A D
= 0101 1010 1101
2) Convert (C9F.2A)16 in to binary
= C 9 F 2 A
= 1100 1001 1111 . 0010 1010
Binary to Hexadecimal Conversion:
Binary number into a hexadecimal number the group of 4-bits, starting from LSB and moving towards MSB for integer part and then replacing each group of four bits by its hexadecimal representation.
1) Convert (110100011111)2 in to hex
= 1101 0001 1111
= D 1 F
2) Convert (11110010.1110)2 in to hex
= 1111 0010 . 1110
= F 2 . E
