Introduction to Number Systems - Octal Number System

The octal number system is called the base-8 system as it has a total of eight digits (0–7). Decimal numbers 0 to 7 match octal, but decimal 8 is octal 10. Octal numbers are easily converted to binary, with each octal digit represented by a three-bit binary number. Octal number system was devised for compact representation of the binary numbers

Convert the given decimal number into Octal, like double-dabble method, where the given integer number is divided by 8 and for fractional numbers, multiply by 8 

1) (175)₁₀  

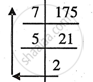
(175)_{10   =}  (257)₈........Ans.

2) (2470)₁₀ 

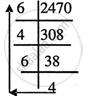
(2470)₁₀  = (4646)_{8............Ans.}

Binary to Octal Conversion: 

• Binary numbers can be converted into equivalent octal numbers by making groups of three bits starting from LSB and moving towards MSB for integer part of the number and then replacing each group of three bits by its octal representation 
• For the fractional part, the groupings of three bits are made starting from the binary point. If required, we can add reading and trailing zeros. 

1) Convert (110100011111)₂  in to Octal 

= 110     100      011     111

=   6        4          3         7

2) Convert (110100101.110011)₂  in to Octal 

= 110    100     101 .  111    011

=   6        4         5   .    7       3

Octal to binary conversion:

Octal numbers can be converted into equivalent binary numbers by replacing each octal digit by its 3-bit equivalent binary

1) Convert (523)₈ in to binary 

=    5      2      3

=  101  010  011

2) Convert (704.01)₈  in to binary 

=   7        0        4            0        1

= 111    000    100   •    000    001

Hexadecimal to Octal Conversion:

To convert a hex number into an octal, first convert hex into a binary, and then make groups of 3-bits from LSB and add zeros on the left and right sides if required. After making the groups, convert each 3-bit binary into an octal equivalent. 

1) (5CA) ₁₆  =   (  ?  )₈

=    5          C          A

=(0101    1100     1010)₂  

=  010    111    001   010

=   2        7        1        2

 (5CA) ₁₆  =  (2712)₈

2) (3B . 2E)₁₆  =  (  ?  )₈

=    3        B          2          E

=(0011   1011  .  0010   1110)₂

= 000   111   011 .  001   011   100

=   0       7      3   .    1        3        4

 (3B . 2E)₁₆   =    (073.134)₈

Octal to Hexadecimal Conversion:

To convert an octal number into a hex, first convert the octal into a binary, and then make groups of 4 bits from LSB and add zeros on the left and right sides if required. After making the groups convert each 4-bit binary into a hex equivalent

1) (537)₈  =  (  ?  )₁₆

=     5         3       7

=  (101    011    111)₂

=0001   0101   1111

=   1         5         F

(537)₈   =   (  15F  )₁₆

2) (53.21)₈  =   (  ?  )₁₆

=   5         3     .      2        1   

= (101    011   .   010     001)₂

= 0010  1011 .  0100  0100

=    2        D    .     4       4

(53.21)₈   =   (2D.44)₁₆