Advertisements
Advertisements
प्रश्न
A(6, 1), B(8, 2) और C(9, 4) एक समांतर चतुर्भुज ABCD के तीन शीर्ष हैं। यदि E भुजा DC का मध्य-बिंदु है, तो ΔADE का क्षेत्रफल ज्ञात कीजिए।
Advertisements
उत्तर
प्रश्न के अनुसार,
एक समांतर चतुर्भुज ABCD के तीन शीर्ष A(6, 1), B(8, 2) और C(9, 4) हैं।
माना समांतर चतुर्भुज का चौथा शीर्ष = (x, y),
हम जानते हैं, कि समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।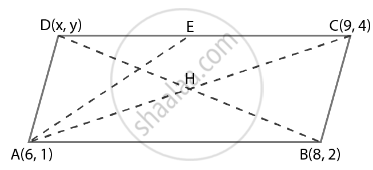
चूँकि, बिंदुओं (x1, y1) और (x2, y2) को मिलाने वाले रेखाखंड का मध्य-बिंदु इस प्रकार दिया जाता है,
`((x_1 + x_2)/2, (y_1 + y_2)/2)`
BD का मध्य-बिंदु = AC का मध्य-बिंदु
`((8 + x)/2, (2 + y)/2) = ((6 + 9)/2, (1 + 4)/2)`
`((8 + x)/2, (2 + y)/2) = (15/2, 5/2)`
तो, हमारे पास है,
`(8 + x)/2 = 15/2`
⇒ 8 + x = 15
⇒ x = 7
और
`(2 + y)/2 = 5/2`
⇒ 2 + y = 5
⇒ y = 3
तो, समांतर चतुर्भुज का चौथा शीर्ष D(7, 3) है।
अब,
पार्श्व का मध्य-बिंदु
DC = `((7 + 9)/2, (3 + 4)/2)`
E = `(8, 7/2)`
∵ शीर्षों (x1, y1), (x2, y2) और (x3, y3) के साथ ΔABC का क्षेत्रफल;
= `1/2`[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
∴ ΔADE का क्षेत्रफल शीर्ष A(6, 1), D(7, 3) और `"E"(8, 7/2)` के साथ,
Δ = `1/2[6(3 - 7/2) + 7(7/2 - 1) + 8(1 - 3)]`
= `1/2[6 xx ((-1)/2) + 7(5/2) + 8(-2)]`
= `1/2(35/2 - 19)`
= `1/2((-3)/2)`
= `(-3)/4` लेकिन क्षेत्रफल ऋणात्मक नहीं हो सकता।
अतः, ΔADE का आवश्यक क्षेत्रफल `3/4` वर्ग इकाई है।
APPEARS IN
संबंधित प्रश्न
कृष्णानगर के एक सेकेंडरी स्कूल के कक्षा X के विद्यार्थियों को उनके बागवानी क्रियाकलाप के लिए, एक आयताकार भूखंड दिया गया है। गुलमोहर की पौध (sapling) को परस्पर 1m की दूरी पर इस भूखंड की परिसीमा (boundary) पर लगाया जाता है। इस भूखंड के अंदर एक त्रिभुजाकार घास लगा हुआ लॉन (lawn) है, जैसाकि आकृति में दर्शाया गया है। विद्यार्थियों को भूखंड के शेष भाग में है फूलों के पौधे के बीज बोने हैं।
(i) A को मूलबिंदु मानते हए, त्रिभुज के शीषों के निर्देशांक ज्ञात कीजिए।
(ii) यदि मूलबिंदु C हो, तो ∆PQR के शीर्षों के निर्देशांक क्या होंगे?
साथ ही, उपरोक्त दोनों स्थितियों में, त्रिभुजों के क्षेत्रफल ज्ञात कीजिए। आप क्या देखते हैं?
एक त्रिभुज ABC के शीर्ष A(4, 6), B(1, 5) और C(7, 2) हैं। भुजाओं AB और AC को क्रमश: D और E पर प्रतिच्छेद करते हुए एक रेखा इस प्रकार खींची गई है कि `"AD"/"AB" = "AE"/"AC" = 1/4` है। ∆ADE का क्षेत्रफल परिकलित कीजिए और इसकी तुलना ∆ABC के क्षेत्रफल से कीजिए।
(प्रमेय 6.2 और प्रमेय 6.6 का स्मरण कीजिए।)
शीर्षों (a, b + c), (b, c + a) और (c, a + b) वाले त्रिभुज का क्षेत्रफल ______ हैं।
यदि बिंदु A(1, 2), O(0, 0) और C(a, b) संरेख हैं, तो ______।
बिंदु (0, 5), (0, –9) और (3, 6) संरेख हैं।
बिंदु A(3, 1), B(12, –2) और C(0, 2) एक त्रिभुज के शीर्ष नहीं हो सकते।
बिंदु A(–6, 10), B(–4, 6) और C(3, –8) इस प्रकार संरेख हैं कि AB = `2/9`AC है।
m का मान ज्ञात कीजिए, यदि (5, 1), (–2, –3) और (8, 2m) संरेख हैं।
एक समबाहु त्रिभुज का परिमाप 60 m है। इसका क्षेत्रफल है
एक समलंब का क्षेत्रफल 475 cm2 है तथा ऊँचाई 19 cm है। इसकी समांतर भुजाओं की लंबाइयाँ ज्ञात कीजिए, यदि एक समांतर भुजा दूसरी समांतर भुजा से 4 cm अधिक है।
