Question

एक त्रिभुज ABC के शीर्ष A(4, 6), B(1, 5) और C(7, 2) हैं। भुजाओं AB और AC को क्रमश: D और E पर प्रतिच्छेद करते हुए एक रेखा इस प्रकार खींची गई है कि `"AD"/"AB" = "AE"/"AC" = 1/4` है। ∆ADE का क्षेत्रफल परिकलित कीजिए और इसकी तुलना ∆ABC के क्षेत्रफल से कीजिए।

(प्रमेय 6.2 और प्रमेय 6.6 का स्मरण कीजिए।)

Answer 1

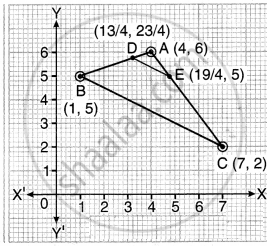
∆ADE और ∆ABC में,

चूँकि `"AD"/"AB" = "AE"/"AC" = 1/4` (दिया है)

एवं ∠DAE = ∠BAC [चित्रानुसार उभयनिष्ठ हैं]

⇒ ΔADE ∼ ΔABC (SAS समरूपता)

⇒ `("ar"("ADE"))/("ar"("ABC")) = ("AD"/"AB")^2 = (1/4)^2` (प्रमेय 6.6 से)

⇒ `("ar"("ADE"))/("ar"("ABC")) = 1/16` ..........(1)

⇒ ar(ADE) : ar(ABC) = 1 : 16

बिन्दु D, AB रेखाखण्ड को 1 : 3 के अनुपात में विभाजित करता है क्योंकि AD : AB = 1 : 4

AD : DB = 1 : 3, इसलिए D के निर्देशांक

x' = `(1 xx (1) + 3(4))/(1 + 3) = (1 + 12)/4 = 13/4`

एवं y' = `(1 xx (5) + 3(6))/(1 + 3) = (5 + 18)/4 = 23/4`

इसी प्रकार E के निर्देशांक

x'' = `(1 xx 7 + 3(4))/(1 + 3) = (7 + 12)/4 = 19/4`

एवं y'' = `(1 xx (2) + 3 xx (6))/(1 + 4) = (2 + 18)/4 = 20/4 = 5`

अब ar(ADE) = `1/2[4(23/4 - 5) + 13/4(5 - 6) + 19/4(6 - 23/4)]`

= `1/2[4 xx 3/4 + 13/4(-1) + 19/4 xx 1/4]`

⇒ ar(ADE) = `1/2[3 - 13/4 + 19/16] = 1/2[[48 - 52 + 19]/16] = 1/2[15/16] = 15/32` वर्ग मात्रक

ar(ABC) = `1/2[4(5 - 2) + 1(2 - 6) + 7(6 - 5)]`

= `1/2[4 xx 3 + (-4) + 7]`

= `1/2[12 - 4 + 7] = 1/2[19 - 4] = 15/2` वर्ग मात्रक

∴ `("ar"("ADE"))/("ar"("ABC")) = (15"/"32)/(15"/"2) = 1/16` ...........(2)

अत: ∆ADE का अभीष्ट क्षेत्रफल = `15/32` त्रक एवं ∆ADE और ∆ABC के क्षेत्रफलों का अभीष्ट अनुपात 1 : 16 है।