Advertisements
Advertisements
प्रश्न
A beam of light consisting of two wavelengths 600 nm and 500 nm is used in Young's double slit experiment. The silt separation is 1.0 mm and the screen is kept 0.60 m away from the plane of the slits. Calculate:
- the distance of the second bright fringe from the central maximum for wavelength 500 nm, and
- the least distance from the central maximum where the bright fringes due to both wavelengths coincide.
उत्तर
(i) Distance of 2nd bright fringe from the central maximum = `(2λ"D")/"d"`
= `(2 xx 500 xx 10^-9 xx 0.6)/(1 xx 10^-3)`
= 6 × 10−4 m
(ii) `("n"λ_1"D")/"d" = (("n" + 1)λ_2"D")/"d"`
Or, nλ1 = (n + 1)λ2
Or, `"n"/(("n" + 1)) = λ_2/λ_1`
Or, `"n"/(("n" + 1)) = 500/600`
∴ n = 5
So, least distance from central maximum = `(5 xx 600 xx 10^-9 xx 0.6)/(1 xx 10^-3)` = 18 × 10−4 m
APPEARS IN
संबंधित प्रश्न
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
Two transparent slabs having equal thickness but different refractive indices µ1 and µ2are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits?
In Young's double-slit experiment, the two slits are separated by a distance of 1.5 mm, and the screen is placed 1 m away from the plane of the slits. A beam of light consisting of two wavelengths of 650 nm and 520 nm is used to obtain interference fringes.
Find the distance of the third bright fringe for λ = 520 nm on the screen from the central maximum.
Two balls are projected at an angle θ and (90° − θ) to the horizontal with the same speed. The ratio of their maximum vertical heights is:
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
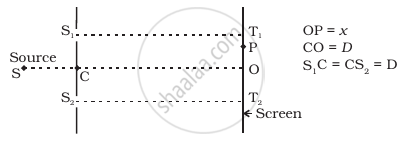
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
Monochromatic green light of wavelength 5 × 10-7 m illuminates a pair of slits 1 mm apart. The separation of bright lines in the interference pattern formed on a screen 2 m away is ______.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
In Young's double-slit experiment, the screen is moved away from the plane of the slits. What will be its effect on the following?
- The angular separation of the fringes.
- Fringe-width.
