Advertisements
Advertisements
प्रश्न
A block of 2 kg is suspended from a ceiling by a massless spring of spring constant k = 100 N/m. What is the elongation of the spring? If another 1 kg is added to the block, what would be the further elongation?
उत्तर
Given,
mass of the first block, m = 2 kg
k = 100 N/m
Let elongation in the spring be x. 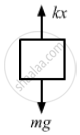
From the free-body diagram,
kx = mg
\[x = \frac{mg}{k} = \frac{2 \times 9 . 8}{100}\]
\[ = \frac{19 . 6}{100} = 0 . 196 \approx 0 . 2 m\]
Suppose, further elongation, when the 1 kg block is added, is \[∆ x\] Then, \[k\left( x + ∆ x \right) = m'g\]
⇒ k \[∆ x\] 3g − 2g = g
\[\Rightarrow ∆ x = \frac{g}{k} = \frac{9 . 8}{100} = 0 . 098 \approx 0 . 1 m\]
APPEARS IN
संबंधित प्रश्न
When a carpet is beaten with a stick, dust comes out of it. Explain.
If the speed of the stone is increased beyond the maximum permissible value, and the string breaks suddenly, which of the following correctly describes the trajectory of the stone after the string breaks?
Define one newton force.
Is it possible for a particle to describe a curved path if no force acts on it? Does your answer depend on the frame of reference chosen to view the particle?
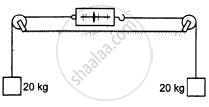
The figure shows a light spring balance connected to two blocks of mass 20 kg each. The graduations in the balance measure the tension in the spring. (a) What is the reading of the balance? (b) Will the reading change if the balance is heavy, say 2.0 kg? (c) What will happen if the spring is light but the blocks have unequal masses?
Consider a book lying on a table. The weight of the book and the normal force by the table in the book are equal in magnitude and opposite in direction. Is this an example of Newton's third law?
Neglect the effect of rotation of the earth. Suppose the earth suddenly stops attracting objects placed near its surface. A person standing on the surface of the earth will.
Three rigid rods are joined to form an equilateral triangle ABC of side 1 m. Three particles carrying charges 20 μC each are attached to the vertices of the triangle. The whole system is at rest in an inertial frame. The magnitude of the resultant force on the charged particle at A is.
In an imaginary atmosphere, the air exerts a small force F on any particle in the direction of the particle's motion. A particle of mass m projected upward takes time t1 in reaching the maximum height and t2 in the return journey to the original point. Then.
A reference frame attached to the earth
(a) is an inertial frame by definition
(b) cannot be an inertial frame because the earth is revolving around the sun
(c) is an inertial frame because Newton's laws are applicable in this frame
(d) cannot be an inertial frame because the earth is rotating about its axis.
A particle stays at rest as seen in a frame. We can conclude that
(a) the frame is inertial
(b) resultant force on the particle is zero
(c) the frame may be inertial but the resultant force on the particle is zero
(d) the frame may be non-inertial but there is a non-zero resultant force
A particle is found to be at rest when seen from a frame S1 and moving with constant velocity when seen from another frame S2. Mark out the possible options.
(a) Both the frames are inertial.
(b) Both the frames are non-inertial.
(c) S1 is inertial and S2 is non-inertial.
(d) S1 is non-inertial and S2 is inertial
A particle is observed from two frames S1 and S2. Frame S2 moves with respect to S1with an acceleration a. Let F1 and F2 be the pseudo forces on the particle when seen from S1 and S2, respectively. Which of the following is not possible?
If you jump barefoot on a hard surface, your legs are injured. But they are not injured if you jump on a soft surface like sand or pillow. Why?
Explain the following :
After alighting from a moving bus , one has to run for some distance in the direction of bus in order to avoid falling .
How does Newton's second law of motion differ from the first law of motion?
Define one Newton.
Give two examples of the following:
Inertia of motion
Two blocks A and B of masses m and 2 m, respectively, are held at rest such that the spring is in natural length. Find out the accelerations of both the blocks just after release.

