Advertisements
Advertisements
प्रश्न
Suppose the ceiling in the previous problem is that of an elevator which is going up with an acceleration of 2.0 m/s2. Find the elongation.
उत्तर
When the ceiling of the elevator is going up with an acceleration 'a', then a pseudo-force acts on the block in the downward direction.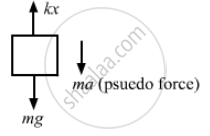
a = 2 m/s2
From the free-body diagram of the block,
kx = mg + ma
⇒ kx = 2g + 2a
= 2 × 9.8 + 2 × 2
= 19.6 + 4
\[\Rightarrow x = \frac{23 . 6}{100} = 0 . 236 \approx 0 . 24 \text{ m }\]
When 1 kg body is added,
total mass = (2 + 1) kg = 3 kg
Let elongation be x'.
∴ kx' = 3g + 3a = 3 × 9.8 + 6
\[ = 0 . 354 \approx 0 . 36 m\]
So, further elongation = x' − x
= 0.36 − 0.24 = 0.12 m.
APPEARS IN
संबंधित प्रश्न
An aircraft executes a horizontal loop at a speed of 720 km/h with its wings banked at 15°. What is the radius of the loop?
You are travelling in a car. The driver suddenly applies the brakes and you are pushed forward. Why does this happen?
An object is placed far away from all the objects that can exert force on it. A frame of reference is constructed by taking the origin and axes fixed in this object. Will the frame be necessarily inertial?
A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block by another string. Find the tensions in the two strings. Take g = 10 m/s2.
An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
Consider the situation shown in the following figure All the surfaces are frictionless and the string and the pulley are light. Find the magnitude of acceleration of the two blocks.

A block A can slide on a frictionless incline of angle θ and length l, kept inside an elevator going up with uniform velocity v in the following figure. Find the time taken by the block to slide down the length of the incline if it is released from the top of the incline.
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12 m/s2. Find the displacement of the block during the first 0.2 s after the start. Take g = 10 m/s2.
A tennis ball and a cricket ball , both are stationary. To start motion in them .
A body of mass m moving with a velocity v is acted upon by a force. Write an expression for change in momentum in each of the following cases: (i) When v << c, (ii) When v → c and (iii) When v << c but m does not remain constant. Here, c is the speed of light.
State Newton's second law of motion. Under what condition does it take the form F = ma?
Use Newton's second law of motion to explain the following instance :
A cricketer pulls his hands back while catching a fast moving cricket ball .
The linear momentum of a body of mass m moving with velocity v is :
A force acts for 10 s on a stationary body of mass 100 kg, after which the force ceases to act. The body moves through a distance of 100 m in the next 5 s. Calculate: The velocity acquired by the body.
Calculate the velocity of a body of mass 0.5 kg, when it has a linear momentum of 5 Ns.
Prove mathematically F = ma
Which of the following has the largest inertia?
Why is it advantageous to turn before taking a long jump?
The position time graph of a body of mass 2 kg is as given in figure. What is the impulse on the body at t = 0 s and t = 4 s.

